Next: 8.6 Spectroscopy with PHT40 Up: 8. Data Processing Level: Previous: 8.4 Photometry

8.5 Mapping

Two dimensional raster and spatially oversampled mapping observations are processed to images in the equatorial (RA and Dec) coordinate system. For the construction of the images it is assumed that a detector footprint (or beam profile) can be represented by a simple `top-hat' function: the emission is 1 inside the detector area and zero outside. In addition, the circular apertures have perfectly circular footprints and the square PHT-P apertures and PHT-C detector pixels are considered to be perfectly square. The positions of each detector pixel per raster point have already been determined in the processing steps described in Section 8.3.3. This section describes the co-addition steps to obtain an image.

Note that in the remainder of this section a clear distinction should be made between detector pixel and image pixel, the former being one of the 9 (for C100) or 4 (for C200) elements in the detector array and the latter being a `picture element' of an image.

The mapping software yields three products:

surface brightness map in units of MJy/sr, this is the average surface brightness of all detector pixel exposures for each image pixel;
uncertainty map in units of MJy/sr, mean brightness uncertainty per image pixel;
exposure map in s, giving for each image pixel the total time that it has been covered by any detector pixel.

8.5.1 Statistical flat-field correction for C100 and C200

Operation: Correct for possible flat-field patterns

Assessment of PHT22 or PHT32 maps have shown that there are systematic flat-field patterns of the C100 and the C200 arrays due to inconsistent surface brightness calibration of the individual detector pixels. The patterns are most prominent in maps with a poor overlap among the individual pixels.

To correct for these patterns a statistical flat-field was applied according to the following steps:

determine for each pixel the 10-percentile of the surface brightness of all raster positions:
compute the flat-field correction ${\char'13}(i)$ for each pixel, by normalising the 10-percentiles to the average:

$\begin{displaymath} {\char'13}(i) = \frac{I^*(i)}{\frac{1}{N}\sum_{i}{I^*(i)}},~~~~~~~~~[~] \end{displaymath}$ (8.13)

where is the number of detector pixels in the array.
apply the flat-field correction to all brightness values :

$\begin{displaymath} I'(i,j)= \frac{I(i,j)}{{\char'13}(i)},~~~~~~~~~[~] \end{displaymath}$ (8.14)

where is the raster step or chopper plateau.

This correction is only applied if the raster map contains 20 or more raster steps for PHT22 raster maps or $\geq$ 20 chopper plateaux for PHT32 maps. The corrections ${\char'13}(i)$ are written in the PGAI product header with keyword FFPF, where is pixel number and filter number in AOT.

8.5.2 Establish image pixel size

Operation: Define the size of the image pixel

The angular dimensions of an image pixel in OLP depend only on the detector subsystem used and is independent on the filter/aperture combination. The values are listed in Table 8.1.

**Table 8.1:** *Image pixel sizes used in OLP. For reference the size of the Airy disc at the shortest detector wavelength is given.*
Detector	Shortest	Airy disc	Pixel
used	wavelength	diameter	size
	[ $\mu$ m]	[arcsec]	[arcsec]
P1	3.2	2.8	8.0
P2	20	17.7	8.0
P3	60	50.3	8.0
C100	70 (C_50)	41.9	15.0
C200	120	101.0	15.0

Based on the image pixel size, the fine-grid is defined to compute the fractional pixel coverage. The optimum fine-grid size in terms of realistic processing times has been decided to be:

$\begin{displaymath} S_{fine~grid} = S_{pixel}/5~~~~~~~~~~~~~~~~~~{\rm [arcsec]} \end{displaymath}$

(8.15)

Ancillary data needed

None, parameters are hardcoded

8.5.3 Establish maximum image size

Operation: Calculate the angular dimensions of the image required to contain the full raster scan in equatorial coordinates.

The maximum size of the image is calculated using the following parameters:

M: the number of raster steps along a raster leg;
N: the number of raster legs;
dM: step size in arcsec along raster leg;
dN: step size in arcsec in between raster legs;
${\alpha}_c,~{\delta}_c$ : the J2000 RA and Dec position in decimal degrees of the raster centre;
${\alpha}_{m,n},~{\delta}_{m,n}$ : the J2000 RA and Dec position in decimal degrees of raster point (m,n), with m= 1...M, and n= 1...N;
D $_{A}$ : the diameter in arcsec of the aperture used, in case of a C-array: the sidelength of the array in arcsec;
$\theta_{chop}$ : the maximum chopper deflection while mapping (only for PHT32 maps).

The centre of the raster scan is defined as the image centre. The dimensions of the frame in equatorial coordinates are derived as follows. For all raster points (m,n) determine:

$\begin{eqnarray*} {\alpha}_{max} = & max( \Delta\alpha(m,n) )\\ {\alpha}_{min... ...ta\delta(m,n) )\\ {\delta}_{min} = & min( \Delta\delta(m,n) ) \end{eqnarray*}$

where:

$\Delta\alpha(m,n)$ : RA component of the difference vector between ( ${\alpha}_{m,n},{\delta}_{m,n}$ ) and ( ${\alpha}_c,{\delta}_c$ )
$\Delta\delta(m,n)$ : Dec component of the difference vector between ( ${\alpha}_{m,n},{\delta}_{m,n}$ ) and ( ${\alpha}_c,{\delta}_c$ )

The components $\Delta\alpha(m,n)$ and $\Delta\delta(m,n)$ are computed using spherical trigonometry. The margins around the raster grid is determined by D $_{A}$ and the maximum chopper deflection $\theta_{chop, max}$ , in raster orientation:

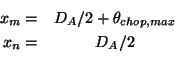
$\begin{eqnarray*} x_{m} = & D_{A}/2+\theta_{chop, max}\\ x_{n} = & D_{A}/2 \\ \end{eqnarray*}$

Then the map dimensions $L_{\alpha}$ and $L_{\delta}$ are computed from:

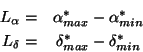
$\begin{eqnarray*} L_{\alpha} = & {\alpha}^*_{max}-{\alpha}^*_{min}\\ L_{\delta} = & {\delta}^*_{max}-{\delta}^*_{min} \end{eqnarray*}$

with

$\begin{eqnarray*} {\alpha}^*_{max} = &{\alpha}_{max}+(\vert x_{m}cos(\phi)\vert... ...ta}_{min}-(\vert x_{m}sin(\phi)\vert+\vert x_{n}cos(\phi)\vert) \end{eqnarray*}$

where $\phi$ is the spacecraft roll angle.

The rectangular image frame is therefore chosen so large that the entire area covered by the detectors in the raster fits inside. Depending on the rotation angle of the raster as well as the sampling step sizes with respect to the size and rotation of the detector, undefined frame areas may be present.

The minimum number of image pixels required to map the whole of the raster area is calculated from the dimensions of the raster and the image pixel size $S_{pixel}$ , as follows:

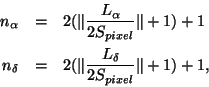
$\begin{eqnarray*} n_{\alpha}& = & 2(\Vert\frac{L_{\alpha}}{2S_{pixel}}\Vert + 1... ...{\delta}& = & 2(\Vert\frac{L_{\delta}}{2S_{pixel}}\Vert + 1)+1, \end{eqnarray*}$

in which $\Vert$ denotes `the integer value of' - i.e. the initial value is rounded down to the nearest integer.

Also calculated at this stage are the angular coordinates of the image pixel origin which is defined as the bottom left hand corner (blhc) of image pixel .

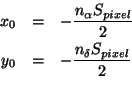
$\begin{eqnarray*} x_{0} & =& -\frac{n_{\alpha}S_{pixel}}{2}\\ y_{0} & =& -\frac{n_{\delta}S_{pixel}}{2}\\ \end{eqnarray*}$

These are used subsequently to translate between the coordinate origin at the centre of the image and the origin of the pixel coordinates.

Finally, the angular coordinates of an image pixel () are:

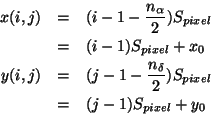
$\begin{eqnarray*} x(i,j) & = & (i-1-\frac{n_{\alpha}}{2})S_{pixel}\\ & = & (i... ...ac{n_{\delta}}{2})S_{pixel}\\ & = & (j-1)S_{pixel} + y_{0}\\ \end{eqnarray*}$

8.5.4 Determination of the coverage by a sky sample in the image

Operation: Map data from a given detector pixel, raster position, and chopper offset combination onto the image.

We define a sky sample to be a sky observation for a given detector pixel, at raster position (m,n), and chopper deflection ${\theta}_{chop}$ . A sky sample has a raster dwell time or chopper dwell time (in case of PHT32 maps).

The fine grid (Section 8.5.2) is used to determine the fractional coverage of the image pixel by the detector footprint. The fine-grid size is chosen such that it is a simple factor of the image pixel size: there is an integral number of grid points per image pixel.

Therefore for each sky sample the following steps are performed:

determine the image pixel range ( $[x_{min},x_{max}],[y_{min},y_{max}]$ ) in which the detector pixel footprint can completely be contained;
for each image pixel contained in this range determine the number of fine-grid positions $N_{fg}$ which fall within the detector footprint.
for each image pixel in the range determine the coverage factor $f_{cov} = N_{fg}/N_{total}$ , where $N_{total}$ is the total number of fine-grid positions on a pixel.

8.5.5 Binning sky samples onto image pixels

Operation: Accumulate the sky samples and derive the average surface brightness, uncertainty and exposure.

The contribution from the ${\rm n^{th}}$ sky sample to the mean brightness, brightness uncertainty, and exposure time at image pixel are denoted $b_{n}(i,j)$ , $u_{n}(i,j)$ and $e_{n}(i,j)$ respectively. The accumulated sums of the contributions from the first pointings are denoted by $B_{n}(i,j)$ , $U_{n}(i,j)$ and $E_{n}(i,j)$ .

The effective exposure time of sky sample at image pixel is the fraction of the image pixel covered by the aperture for a given sample multiplied by the plateau length (Section 8.3.2) converted to seconds, :

$\begin{displaymath} e_{n}(i,j) = f_{cov}(i,j)\,t_{n}~~~~~~~{\rm [s]} \end{displaymath}$

(8.16)

To calculate the total exposure on the image pixel, the contributions from all sky samples are summed. The surface brightness values and the corresponding uncertainties are summed thereby using the exposure times as weights.

$\begin{eqnarray*} E_{n+1}(i,j) = & E_{n}(i,j) + e_{n+1}(i,j)~~~~~~~{\rm [s]}\\ ... ...j) + e_{n+1}(i,j)u_{n+1}^{2}(i,j) ~~~~~~~{\rm [MJy\,sr^{-1}]}. \end{eqnarray*}$

The accumulated sums for all sky samples are used to derive images of total exposure time $E_{total}$ , mean brightness $\overline {B}$ and brightness uncertainty $U_{rms}$ .

$\begin{eqnarray*} E_{total}(i,j) & = & E_{N}(i,j)\\ & = & \sum_{n=1}^{N} e_{n}(i,j)~~~~~~~{\rm [s]} \end{eqnarray*}$

$\begin{eqnarray*} {\overline B}(i,j) & = & B_{N}(i,j)/E_{N}(i,j)\\ & = & \fra... ...}} \sum_{n=1}^{N} e_{n}(i,j)b_{n} ~~~~~~~{\rm [MJy\,sr^{-1}]} \end{eqnarray*}$

$\begin{eqnarray*} U_{rms}(i,j) & = & \left(\frac{1}{E_{N}} {U_{N}(i,j)} \right... ...}^{2}(i,j)} \right)^{\frac{1}{2}} ~~~~~~~{\rm [MJy\,sr^{-1}]} \end{eqnarray*}$

8.5.6 Write image products

Operation: Write a set of complete photometric image products.

First write the product FITS header followed by the processed data in a primary array. The derived surface brightness (in MJy/sr), brightness uncertainty (in MJy/sr) and exposure time (in s) images are stored in separate products.

Detailed product descriptions can be found in Sections 13.4, 13.4.6 (product PGAI), 13.4.7 (product PGAU), and 13.4.8 (product PGAT) for the brightness, uncertainty and exposure time images.

8.5.7 Write PHT-P raster scan photometry products

Operation: Write a complete PHT-P raster photometry product.

Write the product FITS header followed by the processed data in a binary table with each record containing the data for a single filter and sky position.

Detailed product descriptions can be found in Sections 13.4 and 13.4.9 (product PPAS).

8.5.8 Write PHT-C raster scan photometry products

Operation: Write a complete PHT-C raster photometry product.

Write the product FITS header followed by the processed data in a binary table with each record containing the data for a single filter and sky position.

Detailed product descriptions can be found in Sections 13.4 and 13.4.10 (product PCAS).

Next: 8.6 Spectroscopy with PHT40 Up: 8. Data Processing Level: Previous: 8.4 Photometry

ISO Handbook Volume IV (PHT), Version 2.0.1, SAI/1999-069/Dc