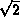 times the
rms HF noise.
times the
rms HF noise.

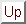


The time fluctuations of the output voltage of any detector
element (hereafter HF, or high frequency noise) are composed of
the readout noise and of the photon noise. The readout noise is
independent of the signal intensity, and slightly dependent on the
electronic gain. The digitization noise is never important, even
with the lowest gain, in the SW channel. The photon noise scales
like the square root of the input signal intensity; the HF noise
shows no detectable pixel to pixel correlation. As a consequence
the rms dispersion of the signal increments between 2 consecutive
readouts, computed over the array, is equal to 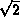 times the
rms HF noise.
times the
rms HF noise.
We have for SW:

where:
S = [ADU/sec_zodi]
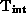 expected signal due to the
Zodiacal light, using Tables in appendix
expected signal due to the
Zodiacal light, using Tables in appendix  , and the zodiacal
background calculation given in appendix
, and the zodiacal
background calculation given in appendix  .
.
n = Number of exposures. (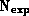 )
)
It is expected that for a given orbit the standard observatory calibration will provide flat-fields with an rms accuracy of 3% and darks with an rms accuracy of 0.5 ADU rms.
The uncertainty of a measurement with the SW array is completely described by combining this HF term with the dark uncertainty and the flat-field uncertainty.