Next: B. List of acronyms Up: ISOLWS DATA USERS MANUAL Previous: 10. Post-processing

A. Detector theory

In this appendix we describe the original (theoretical) approach that was used to extract the photocurrents from the integration ramps. In this scheme, the change in effective bias of the detectors is taken into account by allowing the responsivity S(t) to vary linearly with bias:

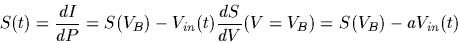$\begin{displaymath}S(t) = \frac{dI}{dP} = S(V_{B})-V_{in}(t) \frac{dS}{dV}(V=V_{B}) = S(V_{B}) - aV_{in}(t) \end{displaymath}$

( A.1)

where V_B is the applied bias voltage. The output voltage V_out(t)- referred for convenience to the input of the FET (i.e. divided by the FET gain) - then obeys the equation

$\begin{displaymath}\frac{dV_{out}(t)}{dt} + \frac{V_{out}(t)}{T_{filter}} = \fr... ... I_{0} \left(1-a \frac{Q_{S}}{C}\right)_{0} e^{-t/T} \right] \end{displaymath}$

( A.2)

where Q_S is the residual charge left on the gate during the re-setting process, H(t) is the Heaviside function and

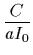T	=	$\displaystyle \frac{C}{aI_{0}}$
T_filter	=	R_filterC_filter
I₀	=	S(V_B)P+Ido	( A.3)

I_do being the dark current immediately following a re-set. If equation A.2 is solved for initial current I_o, the power P falling on the detector can be recovered from the last of equation A.3, provided S(V_B) - obtained from calibration observations - and I_do - obtained from making a measurement with the detectors blanked off - are known.

The solution to equation A.2 is

$\begin{displaymath}V_{out}(t)=\frac{1}{C}H(t)e^{-t/T_{filter}} \left[ Q_{S} + ... ...left(\frac{1}{T}-\frac{1}{T_{filter}}\right)} \right) \right] \end{displaymath}$

( A.4)

To second order in t, equation A.4 becomes

V_out(t) = V_off + A₁ t + A₂ t²

( A.5)

where

V_off	=	$\displaystyle \frac{Q_{S}}{C}$
A₁	=	$\displaystyle \frac{I_{0}}{C}(1-aV_{off})-\frac{V_{off}}{T_{filter}}$
A₂	=	$\displaystyle \frac{1}{2} \left[ \frac{a I_{0}^{2}}{C^{2}} (1 - a V_{off}) \frac{V_{off}}{T_{filter}^{2}} \right]$	( A.6)

If a second-order fit is made to the output of the amplifier, the required current Io can be recovered from the first- and second-order coefficients

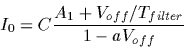$\begin{displaymath}I_{0} = C \frac{A_{1} + V_{off}/T_{filter}}{1-aV_{off}} \end{displaymath}$

( A.7)

As stated above, this is the original scheme for extracting the signal falling on the detectors. It has at least two weaknesses, however. First, the responsivity S is not linear in the effective bias, as assumed in equation A.1. This means that the interpretation of the right-hand side of equation A.7 as the initial photocurrent is suspect, particularly for strong fluxes. Secondly, it is found that the behaviour of the output voltage immediately after re-set is not as given by equation A.3 but is somewhat erratic; in order to deal with this, about 150 ms the data after are ignored in fitting the second-order polynomial to the data, thereby sacrificing potential information. Because of this, it was decided to change the method to the 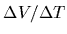$\Delta V/\Delta T$ method that is described in section 6.3.6.

Next: B. List of acronyms Up: ISOLWS DATA USERS MANUAL Previous: 10. Post-processing

ISOLWS Data Users Manual, Issue 5.0, SAI/95-219/Dc