The detector CRE's give systematically different signals for different reset intervals under constant illumination conditions. Analysis of a photometric measurement requires signal information of other measurements such as internal calibration, background, external calibration, target, etc. If these measurements have not the same read-out set-up systematic errors are introduced into the photometric calibration.

It is found that a signal $s(RI,~DAT\_RED)$ obtained with a given reset interval RI and data reduction DR can be converted to a signal $s(RI_x,~DAT\_RED_x)$ of a different CRE settings according to:

$\displaystyle {s(RI_x,~DAT\_RED_x)\,=\,A^x_0(RI_x,DAT\_RED_x,RI,DAT\_RED)}$
		$\displaystyle + A^x_1(RI_x,DAT\_RED_x,RI,DAT\_RED){\cdot}s(RI,~DAT\_RED)~~~~~~ V/s,$	(7.5)

where A^x₀ is the offset value and A^x₁ is the slope in the relationship. Both parameters differ for different detectors. In OLP the reset interval dependence is corrected by transforming all signal values s(RI) to the corresponding values for a reference reset interval $s(RI=\frac{1}{4}\,s, DAT\_RED=1)$ :

$\displaystyle {s(RI=\frac{1}{4}~s,~DAT\_RED=1)\,=\,A_0(RI,~DAT\_RED)}$
		$\displaystyle + A_1(RI,~DAT\_RED){\cdot}s(RI,~DAT\_RED)~~~~~~ V/s,$	(7.6)

where the superscript ^x has been dropped to indicate that the constants A₀ and A₁ refer to the reference reset interval.

For each detector the correction factors A₀ and A₁ are stored in Cal G files PP1RESETI, PP2RESETI, and PP3RESETI for the P detectors and PC1RESETI and PC2RESETI for the C detectors (section 13.6). There is no reset interval correction for PHT-S measurements.

7.3.2 Dark signal subtraction

Dark signals need only to be subtracted for staring mode measurements. Therefore, if the chopper mode is used (see eg. Table 12.2) in AOTs PHT03, PHT22, or PHT40, then the dark signal is not subtracted. In all other cases the dark signal is subtracted from the signal:

$\displaystyle s'({\phi}(t))$	$\textstyle =$	$\displaystyle s({\phi}(t)) - s_{dark}({\phi}(t))$	(7.7)
$\displaystyle s'$	$\textstyle =$	$\displaystyle s~~~~~~~~~~~~~~~~~~~~~ if~chopper~mode~used$	(7.8)

Where $s'({\phi}(t))$ , $s({\phi}(t))$ , and $s_{dark}({\phi}(t))$ ,are the corrected, initial, and dark signal, respectively. The orbital phase ${\phi}(t)$ ranges between 0 and 1 where 0 is the moment of perigee passage and 1 is a full revolution later. The ERD contains the keyword TREFPHA2, which is the orbital phase the start of the measurement. The value for ${\phi}(t)$ in Eqn. 7.8 corresponds to the time mid-point of a chopper plateau.

Ancillary data required:

Dark signal tables for each detector-pixel combination have been derived from dedicated in flight observations. The tables contain a value for the dark signal plus uncertainty (in V/s) for each detector pixel as a function of orbital phase. The data are stored in Cal G files PPDARK (for detectors P1, P2, P3), PC1DARK (contains 9 pixels of C100), PC2DARK (4 pixels of C200), PSDARK (128 pixels of PHT-S), see section 13.7.

7.3.3 Determine chopper position and step number

The telemetry contains the actual chopper position which is recorded every 2 s. The data are provided as voltages and must be converted to a deflection angle. The conversion algorithm can be found in appendix B.3.

The chopper dwell time is directly related to the instrument read-out timing parameters (see section 3.2.4) and is therefore a reliable parameter in the instrument commanding. Using the chopper dwell time corrected for the chopper movement (section 3.6), the moment is determined in ITK units when the chopper should have changed its position.

From the inferred chopper transitions and the ITK of the read-outs the chopper step number is obtained. In principle the same can be done from direct analysis of the chopper position in the telemetry data. The reasons why time is used rather than the chopper position are:

To remove possible contamination by unreliable chopper positions in the data products, a median filter is applied to the positions associated with each integration for a fixed chopper position.

Before the chopper position can be calculated it is necessary to determine the step number I_step within a cycle. The amount of steps in a cycle depends on the chopper mode as follows:

Where steps indicate the number of chopper offset positions at one side of the central field of view (CFOV). The ITK is used to calculate the position in the cycle. In general, for rectangular, sawtooth and triangular chopping, the first chopper position is an ``off-source'' position, the second position is an ``on-source'' position (section 3.6). This is then digitised to the step number I_step as follows:

Ancillary data required:

7.3.4 Signal deglitching

The charges released by a cosmic particle hit cause an effective increase in signal level. Low energetic hits affect only one signal, but high energetic hits can cause several consecutive signals to be higher. A high hit rate can cause the mean signal level in a measurement to increase.

Assuming that the signal distribution is normal on a local scale, a local distribution method is used to filter out signal outliers. The method consists of a `box' sliding along the time axis and local distributions are calculated as it goes. Signals are flagged that are outside a given number of standard deviations from the median for a given local distribution. A signal is eventually discarded in case it is flagged a pre-set number of times. This process is iterated several times.

If the number of available signals is insufficient then a signal is discarded whenever its uncertainty ${\Delta}s_{ph}$ (section 7.2.9) is greater than a given threshold. The controlling parameters of the algorithm are given in Table 7.1.

**Table 7.1:** Parameters for signal deglitching
Parameter	Value	Description
min_deglitch	5	minimum points to apply
max_error	1 V/s	maximum error allowed if number of
		points is less than min_deglitch
n_iter	2	number of iterations of deglitch filter
n_local	20	number of points in local distribution
n_step	1	the number of points to move the `box'
		for the local distribution each time
n_sigma	3	Rejection factor: number of standard
		deviations from local median.
n_bad	2	number of times point has to be flagged
		as `bad' before it is rejected.

The accuracy of this method depends on the glitch frequency and the values of the tuning parameters (ref. Deglitching of ISOPHOT Data by S.Guest [5]). The number of signals affected by glitches is stored in the header of the SPD product (keyword RAMPDEGL, see section 12.3.1.3)

Ancillary data required:

7.3.5 Transient correction

A routine has been implemented which detects the presence of a significant signal transient on a chopper plateau. When a transient is detected, a range of unreliable signals will be flagged. The algorithm is iterative and is applied until either

It is assumed that a detector transient shows up as a trend which causes either a systematic increase or decrease of the signal level. The signal level will eventually become stable in time when the signal reaches its asymptotic limit. The presence of such a trend is detected by applying the non-parametric Mann statistical test to the signals (e.g. [38]). This involves computing a statistic C:

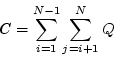$\begin{displaymath} C = \sum_{i=1}^{N-1} \sum_{j=i+1}^{N} Q\end{displaymath}$

(7.9)

for all signals S(i), where i = 1,...,N and N is the number of signals on the chopper plateau. The presence of a transient can be detected by comparing C against the corresponding Kendall k-statistic for a given confidence level.

Alternatively, as the number of signals is generally large, it is more convenient to compute the statistic C(*) which can be compared with the quantile of a normal distribution:

$\begin{displaymath} {C(*) = \frac{C}{\sqrt{N(N-1)(2N+5)/18}}}~.\end{displaymath}$

(7.10)

The result, C(*), is tested against the null hypothesis which assumes absence of drift. This corresponds to a critical value of C(*)< 1.645 for ${\alpha} = 0.05$ . A test is made on whether the drift is up (C(*)<1.645) or down (C(*)>-1.645).

The algorithm initially performs the test on all available signals on a chopper plateau. If the null hypothesis is rejected then the test is performed on the second half of the data and the first half is rejected. If the null hypothesis is again rejected then the second half of the second half is tested etc. The iteration stops either when the null hypothesis is accepted or when there are too few signals (N $\leq$ N(min)) to apply the test. Information on the outcome of the procedure is stored per chopper plateau by setting the pixel status flags 2 (``drift fit applied successfully'') or 4 (``drift fit may not be accurate'') in the SPD records (see Section 12.3.12).

Ancillary data required:

7.3.6 Averaging signals of same instrument set-up

To increase the signal-to-noise ratio, all valid signals on a single chopper plateau are averaged. The following formula is applied:

$\begin{displaymath} {\langle s\rangle} = {\frac{\sum_{1}^{N}w_{i}\times s'_{i}} {\sum_{1}^{N}w_{i}}}~~~~~~~~~~V/s,\\ \end{displaymath}$

(7.11)

where N is the total number of valid signals on the plateau and $w_{i}={\Delta}^{-2}s_{ph}$ is the statistical weight of each signal obtained from its associated statistical uncertainty propagated from the previous signal processing steps. The value for N is stored in an SPD record PxxSNSIG.

The plateau average is either (1) the average of the signals which are not flagged as drifting according to the test described in section 7.3.5 or (2) the average of the last 7 signals of the plateau in case the test fails.

If it is not possible to calculate a weight for any of the signals on a plateau then all signals will have a weight $\rm w_{i}$ = 1 assigned. This can happen when the ramps consist of only 2 useful read-outs. If no weight can be calculated for a subset of the signals on the plateau then these will be weighted out by setting $\rm w_{i}$ = 0.

The uncertainty on the average signal is derived from the rms of the individual signals:

$\begin{displaymath} {\Delta \langle s \rangle = \sqrt{\frac{\sum_{1}^{N}w_{i}\ti... ... - \langle s \rangle)^{2}} {(N-1)\sum_{1}^{N}w_{i} }}}~~~~V/s.\end{displaymath}$

(7.12)

Ancillary data required:

7.3.7 Obtaining the median of all photo-currents

The signal distribution can be non-gaussian due to signal transients or due the presence of many positive signal outliers caused by glitches which have not been filtered out completely. In such case, the median signal is a better estimate for the signal per chopper plateau than the average. The median and the quartiles in conjunction with the weighted average should retain information on non-gaussion signal distribution. For a gaussian distribution the median is close to the average, and the quartiles fall within the uncertainty interval.

Therefore the median ( ${\rm \langle s_{ph} \rangle}^M$ ) and first and third quartile of all available signals are calculated. Different from the computation of the weighted average, the determination of the median, first, and third quartile values does not exclude signals that are flagged as unreliable by the signal deglitching or transient correction.

Ancillary data required:

7.3.8 Correction for chopper vignetting

The throughput of the ISO and ISOPHOT optics depends on the chopper deflection. The level of variation is of order of a few percent for the maximum chopper deflection in case of the C100 and C200 subsystems. Especially for weak sources on a strong background this phenomenon can cause spurious detections or negative signals for some pixels on the arrays.

For each average and median signal $\langle s \rangle$ the correction $t_{\rm chop}$ is applied:

$\begin{displaymath} {\langle s_c \rangle} = t_{chop}(filter, pixel, chopper~deflection) {\times} {\langle s \rangle}~~~~~~~~~~~~~V/s.\end{displaymath}$

(7.13)

Ancillary data required:

The correction for C100 and C200 are stored in the Cal G files PC1VIGN and PC2VIGN, see section 13.8. Since for the P detectors no measureable ( $\gt 2\%$ ) effect could be found, the correction factors in the designated Cal G files PPxVIGN (x= 1, 2, 3) have been set to 1.

7.3.9 Correction for chopped signal losses

For chopped observations the signal is modulated by the chopper between source and background. Due to the long response time of the detectors relative to the duration of a chopper plateau, the signal on a chopper plateau cannot stabilize. The resulting signal difference is less than the signal difference between two stabilized source and background measurements in staring mode.

The computation of the difference flux between the on and off chopper plateaux is beyond Derive_SPD (cf. section 7.1) and reserved for Derive_AAR. As a consequence, in this processing step only the correction factors are obtained by reading the relevant CalG files based on the value of t_chop. The correction factor is subsequently transferred to Derive_AAR processing via the SPD product in the header of the FITS file. The keyword is ``CHCjRi'' (Chopper correction factor) where i=[1, no. of pixels] and j=[1, no. of measurements].

As will be described in section 7.4 the individual chopper plateaux are calibrated using the default responsivity without any correction for losses.

Ancillary data required:

The correction factors are stored in Cal G files PPCHOPCOR, PC1CHOPCOR, and PC2CHOPCOR for the P, C100 and C200 detectors respectively. The structure of the Cal G files are described in section 13.9.

7.3.10 Ramp statistics in PHT SPD and Cal-A headers

Useful statistics about readout and signal discarding collected along the signal processing chain is made available to the observer. The statistical information is stored in the SPD product headers.

Staring	1
Rectangular	2
Sawtooth	$2 \times steps + 1$
Triangular	$4 \times steps$

Q = sign(S(j) - S(i))	=	+1	if S(j) > S(i)
	=		if S(j) = S(i)
	=	-1	if S(j) < S(i)

7.3 Signal Processing

7.3.1 Reset interval correction

7.3.2 Dark signal subtraction

Ancillary data required:

7.3.3 Determine chopper position and step number

Ancillary data required:

7.3.4 Signal deglitching

Ancillary data required:

7.3.5 Transient correction

Ancillary data required:

7.3.6 Averaging signals of same instrument set-up

Ancillary data required:

7.3.7 Obtaining the median of all photo-currents

Ancillary data required:

7.3.8 Correction for chopper vignetting

Ancillary data required:

7.3.9 Correction for chopped signal losses

Ancillary data required:

7.3.10 Ramp statistics in PHT SPD and Cal-A headers

Ancillary data required: