

Next: 3 Impact on the
Up: Introduction
Previous: 1 Conclusions
In a sense we are quite lucky as the observations that were mostly
affected by the flare turn out to have almost identical counterparts
done in more normal conditions during revolutions 222 and 224. I have
thus extracted these data from the archive and used it to assess the
quality of CAM data on revolution 722 and 723. Table 1
lists the relevant parameters of the set of observations considered here.
Since CAM is an imager, and since the event we are expecting is a
particle shower, the easiest way to get a rapid idea of the event's
impact is to look at CAM's images (here corrected for dark with the
CALG dark). This is done on figure 1 where I show 64
images of 22202606, i.e. normal 5.04 integrations, and 64 images of
72200108, identical configuration though it is clear that the number
of particles has ``somewhat'' increased. The change in aspect from one
image to the other is not due to a rapid background variation but to
the fact that the lookup table is adjusted each time to the full
intensity of the image, which in turn is totally dominated by the
glitches.
The second CAM observation on revolution 722 is identical to the first
one, both in setup and in degradation, thus for the rest of this
report I will not consider it. The 5.04s observation that was done
on revolution 723 has the same aspect as that of revolution 222, thus
to save space I will not display it. Similarly, there are no
visible differences between the images taken at 10.08s in revolution
224 and those from 723, apart from the change in background level (a
factor of  4). But there is more here than meets the eye.
4). But there is more here than meets the eye.

Figure 1: Dark corrected images in LW3, 5.04s integration,
6''/pix for a ``normal'' revolution on the left and during
revolution 722 on the right. The raw 10.08s data taken either on
revolution 224 or 723 show much less glitches than what can be seen here
during revolution 722! The display actually does not do justice to the glitch
fireworks of revolution 722...
For deglitching, I have only used the multi-resolution median
transform algorithm (also called mm or mr1d_deglitch) as it is the best
adapted to that sort of data: constant background, isolated point
sources, glitches leaving long lasting imprints on the
detector. Furthermore as the sources are extremely weak I can relax
the constraint on the number of scales inspected for glitches.
For the LW3 observations, with 20 exposures per raster positions, the
scale parameter can be raised to 4. As for the sigma parameter,
experience shows that at 5.04s integration time, a value of 6 is a
good choice (efficient deglitching and few noise spikes
removed). Applying these parameters on revolution 222 indeed gives
excellent results. 5% of the array is affected by glitches.
The same parameter set on revolution 723 also produces quite
satisfatory results with again about 5% of the detector being masked.
This is no longer the case for revolution 722. This choice of
parameters removes part of the glitches, but only to show that more
are still remaining on the array. In fact to clean the array to an
acceptable (see later in what sense) level I had to perform 2
successive rounds of deglitching up to scale number 4 and down to
3-  deviations. It is worth mentionning here that such a
processing would very likely affect source signals in the field,
except maybe the faintest ones, and is therefore not recommended when
one has science in mind. At the end of this process, 36% of the array
has been rejected due to glitches and inspection of the data shows (see
e.g. fig. 2) that glitches still remain on the detector.
deviations. It is worth mentionning here that such a
processing would very likely affect source signals in the field,
except maybe the faintest ones, and is therefore not recommended when
one has science in mind. At the end of this process, 36% of the array
has been rejected due to glitches and inspection of the data shows (see
e.g. fig. 2) that glitches still remain on the detector.
Therefore we can conclude from these numbers that we have seen during
revolution 722 an increase in the rate of glitches by a factor of at
least 7, and probably around 10. We were back to a normal rate of
glitch impact at the start of revolution 723.
For the LW2 data, taken at 10.08s, the small number of exposures
taken would restrict the number of scales to be used for deglitching to
3. With such a small number, it is impossible to properly deglitch
either the revolution 224 or 723 data with the multi-resolution
method. Thus I have assumed that the sources are faint enough so that
they do not show on individual frames and thus I can increase the
number of scales up to 4. I also have had to decrease the sigma
parameter to 3 to produce efficient deglitching for both
revolutions. Thus the final setup was Nscale=4 and
Nsigma=3 for both revolutions.
It produces very similar results on both revolutions, i.e. most of the
glitches are gone, though long-lasting ones are obviously still there,
and approximately 10% of the array is flagged as glitched, indicating
once again a normal behavior in terms of glitch rate for revolution
723.
Assuming one can deglitch the data obtained during such a storm, one
may wish to know whether the resulting data can be used
scientifically, i.e. is CAM in a state where the calibration
measurements apply? The answer here is quite certainly no. The global
increase in the number of glitches imply a similar increase in the
number of glitches affecting the gain of the detector. As a result the
latter varies quite significantly and stochastically during the
observations, on scales as small as 1 minute. Therefore the data will
be quite difficult, if not impossible, to calibrate.
This rapid variation is illustrated in figure 2 for the
5.04s integrations, and figure 3 for the 10.08s
integrations. On these figures I have plotted the dark-corrected,
deglitched as indicated above, signal from a representative pixel near
the center of the array. For the 5.04s integrations the solid line
is for revolution 722, the dash-dotted one for revolution 723 and the
dotted one for revolution 222. For the 10.08s integrations, we have
no data on revolution 722, so the solid line is for revolution 723 and
the dotted one for revolution 224. Offsets have been used to put
all these signals on the same plots.
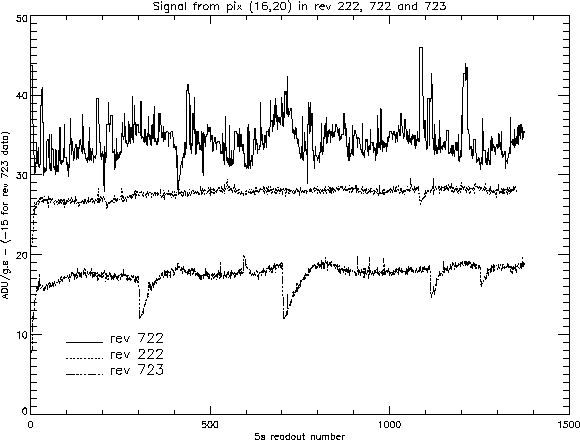
Figure 2: For the 5.04s readouts, signal from a representative pixel
(16,20) in the three revolutions used here: 722, solid line, 723
dot-dashed line and 222, dotted line. 15 ADU/g.s have been subtracted
from rev 723's output to place it on the same graph. Variation of the
mean flux level between revolutions is due to the fact that the
zodiacal light contribution depends on the date of the observation and
pointing direction.
On figure 2, where I remind that no multiplicative
scaling has been applied, the degradation of data quality is
obvious. More precisely, signal from revolution 722 is highly
unstable, probably because glitches with positive tails (e.g. the
pseudo-sources near readout number 1100 and 1200) pile up in time with
glitches with negative tails (e.g. at readout number 400). It is
doubtful that any photometry can be done with such an unstable
array. The contrast is stricking with signal from revolution 222 or
even with that of revolution 723.
It is also apparent on this graph, that, though the improvement is
dramatic from revolution 722 to 723, we still are not in ideal
conditions: there is a larger number of glitches with negative
tails. In principle, faint source analysis is able to deal with these
glitches.
A more quantitative assessment of the data quality can be made by
comparing the ratio of mean intensity in the cube over rms in the data
cube, a sort of Signal to Noise (S/N) ratio, for these three
observations. To do that, I have flat-fielded the data with the CALG
flat-field, and, since it is not very adequate on the edges of the
detector, I have used only the area (10:21,10:21).
Table 2 summarizes the results obtained this way.
|
TDT | 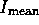 | 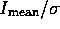 |
| 22202606 | 27.8 | 36.1 |
|
72200106 | 35.5 | 11.5 |
|
72300706 | 33.9 | 30.3 |
| 22401403 | 1.60 | 11.8 |
|
72300605 | 6.90 | 14.4 |
Table 2: Mean intensity, and ``S/N on the background'', for the
observations studied here. Note that the two 10.08s observations were
not done with the same lens, 3''/pix for the 224 observation and
6''/pix for the 723 one. As a result the mean flux is almost exactly
a factor a 4 higher but the S/N clearly does not follow that trend: we
expect a factor of 2, while we only find a factor of 1.22. Also note
the dramatically low S/N value for rev 722 compared to both
revolutions 222 and 723.
For the 5.04s observations, the setup is strictly identical in the
three observations, and the background only changes by 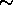 10%,
which should have a minimal impact on the resulting S/N. Yet one can
clearly see that this ratio has decreased by a factor of 3 from
revolution 222 to revolution 722. This reinforces the previous
statement that is quite useless to try and do science under such
conditions. As was also hinted at before, we can see that revolution
723 represents a noticeable step toward full recovery but we are not
quite there yet: the S/N is still significantly lower, reflecting the
higher number of glitches with negative tails.
10%,
which should have a minimal impact on the resulting S/N. Yet one can
clearly see that this ratio has decreased by a factor of 3 from
revolution 222 to revolution 722. This reinforces the previous
statement that is quite useless to try and do science under such
conditions. As was also hinted at before, we can see that revolution
723 represents a noticeable step toward full recovery but we are not
quite there yet: the S/N is still significantly lower, reflecting the
higher number of glitches with negative tails.
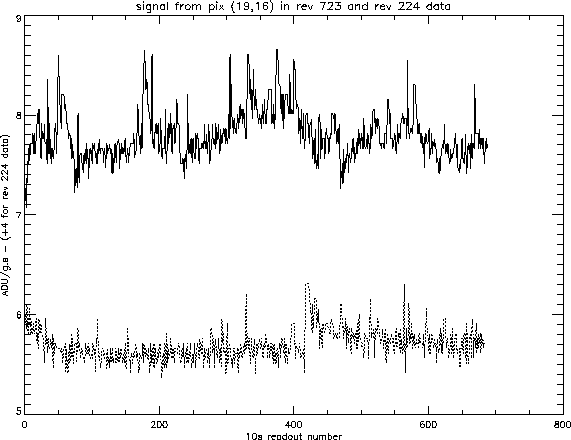
Figure 3: For the 10.08s readouts, signal from a representative pixel
(19,16) in the two revolutions used here: 723, solid line, and 224,
dotted line. 4 ADU/g.s have been added to rev 224's output to place it
on the same graph. Variation of the mean flux level between
revolutions is mostly due here to the two different pixel
field-of-views used.
For the 10.08s integration time, we have no data taken on revolution
722. However, comparison of 10.08s data from revolution 224 and 723
with their corresponding 5.04s data (i.e revolution 222 and 723)
shows that the trends should be quite similar. As can be seen on
figure 3, data from revolution 723 are still quite
noisy, indicating that the array still sees a higher number of
glitches with tails compared to normal operating conditions. This is
confirmed by the comparison of S/N in table 2: as the
flux increases by a factor of 4 due to the use of the 6''/pix lens,
we expect and increase of the S/N by a factor of 2 . Such is not the case, the
increase is only a factor 1.22. The data from revolution 723 appears
significantly more chaotic in figure 3 than in
figure 2. That is probably due to two facts: (1) the
10.08s observation is done before the 5.04s one (both last
approximately 2 hrs) and (2) the x axis is not equivalent on
both graphs, that of figure 3 should be multiplied by 2
to be brought on the same scale as that of figure 2.
. Such is not the case, the
increase is only a factor 1.22. The data from revolution 723 appears
significantly more chaotic in figure 3 than in
figure 2. That is probably due to two facts: (1) the
10.08s observation is done before the 5.04s one (both last
approximately 2 hrs) and (2) the x axis is not equivalent on
both graphs, that of figure 3 should be multiplied by 2
to be brought on the same scale as that of figure 2.


Next: 3 Impact on the
Up: Introduction
Previous: 1 Conclusions
Marc Sauvage



