The filters available for PHT-P and
PHT-C are
listed in Tables 2.2 and 2.7.
Let ![]() be the actual bandpass,
which is the filter transmission function convolved with the relative
spectral detector
response2.1; then
the central wavelength
be the actual bandpass,
which is the filter transmission function convolved with the relative
spectral detector
response2.1; then
the central wavelength
![]() , the filter width
, the filter width
![]() , and the average relative system response
, and the average relative system response ![]() are defined as:
are defined as:
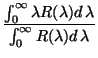 |
(2.2) | ||
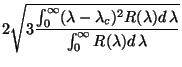 |
(2.3) | ||
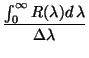 |
(2.4) |
![]() is the width of a rectangular filter having the same
integrated relative system response as the actual bandpass2.2. The relative response curves
of all bandpasses are shown in Appendix A.2.
Note that due to the large wings of especially the long wavelength
filters, the rectangular widths (given in Tables 2.2 and 2.7) are significantly different from the full width at
half maximum. Some useful filter combinations, including comparisons
with IRAS filters, are illustrated in Appendix A.2.
is the width of a rectangular filter having the same
integrated relative system response as the actual bandpass2.2. The relative response curves
of all bandpasses are shown in Appendix A.2.
Note that due to the large wings of especially the long wavelength
filters, the rectangular widths (given in Tables 2.2 and 2.7) are significantly different from the full width at
half maximum. Some useful filter combinations, including comparisons
with IRAS filters, are illustrated in Appendix A.2.