next up previous contents index
Next: 6.4 Comparison with Models Up: 6. ISO Cross-Calibration Previous: 6.2 Internal Cross-Calibration

Subsections


6.3 External Cross-Calibration


6.3.1 Comparison with IRAS


6.3.1.1 SWS versus IRAS photometry

A large number of astronomical sources observed with SWS were also detected by IRAS in the 12 and 25 $\mu $m bands and are included in the IRAS Point Source Catalogue.

In order to compare the absolute flux calibration of IRAS and ISO SWS we searched the ISO Data Archive for observations made with ISO at the same positions of the sky, allowing a maximum offset of 1.5$^{\prime}$. This way, we found up to 556 different pointings in the ISO Data Archive containing SWS01 observations corresponding to around 400 different IRAS sources.

Unfortunately, many of the sources in this sample had to be discarded because they were known to be slightly extended sources or strongly variable. Extended sources may introduce uncertainty in the results; first, because the SWS calibration is based on point source flux calibration and correction factors are needed to derive their actual absolute flux and, second, because many of these extended sources are usually located in areas of the sky with a complex structure at infrared wavelengths, which complicates even more the problem.

Sources which look extended to SWS are easily recognised because the spectra show strong flux jumps between bands coincident with changes in the aperture size, as we have already shown in Figure 6.1 (bottom panel).

Concerning variability, we know that many of the stars observed by ISO are characterised by their strong photometric variability. Many of them are pulsating stars in the Asymptotic Giant Branch (AGB) phase evolving into planetary nebulae. Some others are young stellar objects which may also be variable (although in this case the amplitude of the variations in this spectral range is usually not very large).

In spite of all these limitations, we ended up with a list of still more than 250 individual observations susceptible to be used for cross-calibration with the IRAS photometry at 12 and 25 $\mu $m, corresponding to more than 100 different astronomical sources, covering a wide range of spectral shapes and brightness.

Each of these 250 individual OLP Version 10 SWS spectra were retrieved from the ISO Data Archive and further processed with ISAP Version 2.1. Basically, bad data points affected by glitches were identified and removed from the spectra using the available tools in ISAP and what we can call `ISO SWS photometry' was performed at 12 and 25 $\mu $m with the help of the syn_phot application of ISAP, which simply convolves the ISO spectrum with the transmission profile of the IRAS filters at 12 and 25 $\mu $m and assigns a monochromatic flux at these two wavelengths under the assumption that the source SED shape is of the form $\nu$ $\times$ f$_{\nu}$ = constant, or equivalently $\lambda$ $\times$ f$_{\lambda}$ = constant, in the same way as IRAS did.

In Figure 6.14 we show the results obtained at 12 $\mu $m. At first sight, the conclusion is that, in general, ISO SWS synthetic photometry and IRAS photometry at 12 $\mu $m are consistent within the 15% level in most cases independent on the flux level considered (from few Jy to several thousand Jy), with only a few sources showing a slightly worse agreement ($\sim$25-30%) at low flux levels (below 25 Jy).

Figure 6.14: ISO SWS synthetic photometry at 12 $\mu $m derived from OLP Version 10 data products compared to IRAS photometry at the same wavelength. The dashed red line represents a 15% discrepancy level
\resizebox {14.3cm}{!}{\includegraphics{iras12_sws_olp10.ps}}

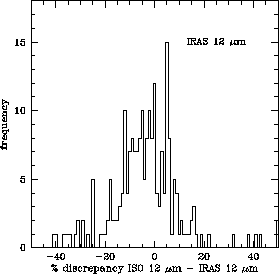
Figure 6.16 (left panel) shows the distribution of the discrepancies found between the ISO SWS synthetic photometry and IRAS photometry at 12 $\mu $m. Taking the mean absolute flux level of all the measurements taken with SWS and IRAS at 12 $\mu $m the zero-point consistency is found to be better than 2%.

Note that the overall distribution is, however, slightly asymmetric. In the absence of other known calibration problems, the few obvious outliers towards positive values (ISO fluxes overestimated with respect to IRAS) might correspond to variable sources not recognised as such in the sample (and, thus, not purged) detected close their maximum brightness by ISO, while those towards negative values (ISO fluxes underestimated with respect to IRAS) are interpreted as a combination of previously unknown variable sources (caught this time during minimum brightness by ISO) and slightly bad-pointed observations which have partially escaped from detection.

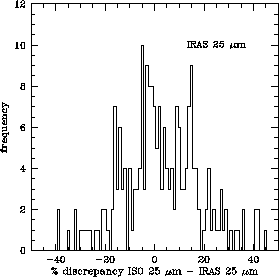
A very similar result is obtained at 25 $\mu $m, as we can see in Figure 6.15. The level of agreement is again in most cases within 15% for strong sources (above 50 Jy), with very few exceptions, although it becomes also slightly worse for low flux levels (typically within 25-30% for fluxes below 15-20 Jy). Comparing the absolute flux level of all the measurements performed with SWS and IRAS at 25 $\mu $m the zero-point consistency is found to be better than 1% (for the derivation of this number, the measurements at 25 $\mu $m corresponding to sources with an absolute flux level at this wavelength below 15 Jy were excluded).

Figure 6.15: ISO SWS synthetic photometry at 25 $\mu $m derived from OLP Version 10 data products compared to IRAS photometry at the same wavelength. The dashed red line represents a 15% discrepancy level.
\resizebox {14.3cm}{!}{\includegraphics{iras25_sws_olp10.ps}}

In this case, however, the overall distribution of discrepancies plotted in Figure 6.16 (right panel) is not asymmetric, in contrast with what was found at 12 $\mu $m. The number of strongly underestimated fluxes by ISO with respect to IRAS are in this case more or less similar to the number of overestimations. The few obvious outliers at both sides of the distribution are actually the same sources observed as outliers at 12 $\mu $m supporting the hypothesis that they may be variable stars. Thus, we interpret the symmetry observed in this case as the consequence of the smaller number of badly pointed observations at this wavelength, probably because of the larger apertures used by SWS bands 3 and 4, which lowers the probability of missing part of the incoming flux from a point source when it is observed slightly off-axis.

Figure 6.16: Distribution of the discrepancies found between the ISO SWS synthetic photometry at 12 $\mu $m (left) and 25 $\mu $m (right) derived from OLP Version 10 data products compared to the IRAS photometry
\resizebox {6.5cm}{!}{\includegraphics{stat_12.ps}} \resizebox {6.5cm}{!}{\includegraphics{stat_25.ps}}


6.3.1.2 LWS versus IRAS photometry

A similar analysis was performed by Chan et al. 2001, [20] considering all sources observed with ISO LWS in the grating scan mode (LWS01 AOT) for which there was also available photometry at 100 $\mu $m in the IRAS Point Source Catalogue.

In order to compare the absolute flux calibration of IRAS and ISO LWS the ISO Data Archive was searched for observations made with ISO at the same positions of the sky, allowing a maximum offset of 2$^{\prime}$. The objects were selected according to the additional following criteria:

1.
IRAS flux density qualities $\ge$2 in the 60 and 100 $\mu $m bands

2.
LWS data showing no fringes -- to avoid sources with a strong cirrus background and/or extended objects

3.
F$_{\nu}$(100 $\mu $m) $<$ 1000 Jy -- to avoid detector non-linearities

4.
F$_c$/F$_s$ $<$ 0.5, where F$_c$/F$_s$ is the flux density ratio of cirrus and source

5.
IRAS CIRR3 $\le$ 254 MJy/sr and no strong cirrus background on the IRAS Sky Atlas Maps or in the LWS parallel maps at 100 $\mu $m (LW1 detector).

6.
source is not a known variable source

A total number of 170 different pointings were found in the ISO Data Archive containing LWS01 observations satisfying the above criteria corresponding to 120 different IRAS sources. They all were included in this cross-calibration analysis as test cases, covering a wide range of spectral shapes and brightness.

The OLP Version 10 LWS grating spectra were retrieved from the ISO Data Archive and further processed with ISAP Version 2.1 prior to their comparison with the IRAS photometry at 100 $\mu $m. Bad data points affected by glitches were removed from the spectra using the available tools in ISAP. A few sources had to be corrected also for the so-called `near-infrared leak'. This is an instrumental effect which produces false strong features at $\sim$53$\mu $m and $\sim$105 $\mu $m on the LWS spectra of sources with a bright near infrared counterpart. These features can easily be removed by fitting a power-law to the underlying continuum and assuming they have a Gaussian profile, which is a very good aproximation to their real shape (see ISO Volume III of the Handbook on LWS, [68] for more details).

ISAP was also used to perform the equivalent `ISO LWS photometry' at 100 $\mu $m of all the 120 sources contained in our new cross-calibration sample. This was done using again the syn_phot application, which convolves the ISO spectrum with the transmission profile of the IRAS 100 $\mu $m filter. This assigns a monochromatic flux at this wavelength under the assumption that the source SED shape is of the form $\nu$ $\times$ f$_{\nu}$ = constant, or equivalently $\lambda$ $\times$ f$_{\lambda}$ = constant, in the same way as IRAS did.

The main problem which affects our cross-calibration comparison is the cirrus contamination. The infrared sky is characterised by emission at 100$\mu $m from interstellar dust on all spatial scales. In spite of the restrictions applied to the selected sources, a significant chance exists that some of them can still be affected by components of this long-wavelength emission on point source scale. While the IRAS photometric fluxes quoted in the Point Source Catalogue are already corrected for this background `cirrus' emission, this is not the case of the photometry derived from LWS data, which includes this background contribution. Therefore, it is necessary to apply a correction either to LWS data or to the IRAS photometry before making any cross-calibration comparison.

Two methods can be applied to perform this `cirrus correction'. Both recovery procedures are only an approximation:

-
Method 1: based on the restoration of the original IRAS flux density at 100 $\mu $m uncorrected for cirrus (i.e. F$_c$ + F$_s$) using the value of CIRR2 listed in the IRAS Point Source Catalogue, which is directly related via Equation 6.1 to the value of F$_c$/F$_s$. As we have already mentioned in Section 6.2.2.4 CIRR2 is an integer in the range from 1 to 9. CIRR2 values less than 4 indicate little or no cirrus contamination. CIRR2 values larger than 5 indicate the presence of bright cirrus emission heavily contaminating the source photometry.

-
Method 2: based on the removal of the cirrus contamination from the ISO-LWS synthetic photometry using the CIRR3 values listed in the IRAS Point Source Catalogue. CIRR3 is the total surface brightness of the sky surrounding a source in a 0.5$^{\circ}$ beam at 100 $\mu $m clipped to exclude values larger than 254 MJy/sr. LWS calibration is based on point sources, so those that sit on a significant background will require this correction before they can be compared with the IRAS photometric values in the Point Source Catalogue. To perform this correction requires the knowledge of the ISO LWS beam; that is, the effective solid angle of the LWS detectors and the so-called `extended source correction factors', both of which are given in the ISO Handbook Volume III on LWS, [68]. The main problem of this whole procedure is that in regions with bright cirrus emission, the CIRR3 value may overestimate grossly the true background flux local to the source.

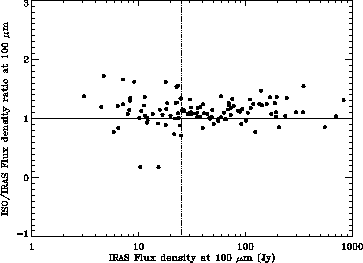
Figure 6.17 shows the distribution of ISO/IRAS flux density ratios at 100 $\mu $m as a function of the IRAS flux density at 100 $\mu $m in a logarithmic scale using the two different methods above mentioned. The results obtained suggest that, in spite of the uncertainties induced by the sometimes large (and inaccurate) correction factors needed to make this comparison, there is a reasonable good agreement between ISO and IRAS at 100 $\mu $m in most cases (within 30%).

Figure 6.17: The LWS/IRAS flux density ratios at 100 $\mu $m as a function of the IRAS flux density at 100 $\mu $m using Method 1 (top) and Method 2 (bottom). The vertical dashed line represents an arbitrary limit below which LWS accuracy becomes dominated by inaccurate dark current subtraction. Note the higher fluxes detected by ISO with respect to IRAS at high flux levels in both cases (from Chan et al. 2001, [20]).
\resizebox {8.2cm}{!}{\includegraphics{ChanSJ_4.eps}}
\resizebox {8.2cm}{!}{\includegraphics{ChanSJ_5.eps}}

However, ISO flux calibration is found to give systematically 12.5% higher fluxes respect to IRAS (if we take the mean value), independent on the method used. A similar discrepancy (11.3%) was reported in the LWS OLP Version 10 Scientific Validation Report (Lim et al. 2001, [114]), where the calculations were restricted to a short list of low background sources, suggesting that the problem is not related to a wrong background subtraction.

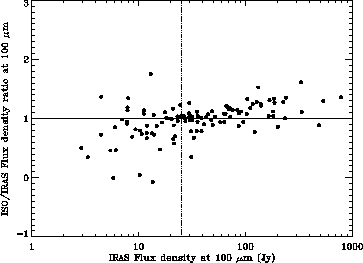
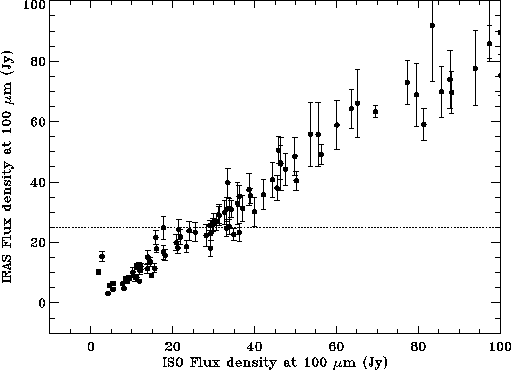
In order to analyse more in detail the problem we have plotted in Figure 6.18 the results of the same cross-calibration comparison in a linear scale and only including sources with IRAS flux densities at 100 $\mu $m below 100 Jy using Method 1. Interestingly, the distribution shows the existence of at least 2 different turning points leading to three different regimes. The first regime is followed by sources with ISO fluxes below 25 Jy. These are the sources showing the higher degree of consistency with ISO in terms of absolute flux level, although the dispersion is very high at these low flux levels, as expected, due to inaccurate dark current subtraction. A second regime is followed by sources well detected by ISO with fluxes at 100 $\mu $m between 25 and 75 Jy. These sources show systematically 10-15% higher ISO fluxes compared to IRAS with a dispersion of only 20%. And there seems to be even a third regime beyond 75 Jy which shows an even larger systematic discrepancy (up to 20%) with a similar dispersion. The same behaviour, although not shown here, is observed when we use Method 2.

Figure 6.18: ISO LWS synthetic photometry at 100 $\mu $m compared to IRAS photometry at the same wavelength for sources with IRAS flux density at 100 $\mu $m less than 100 Jy, using Method 1. The horizontal dashed line represents an arbitrary limit below which LWS accuracy becomes dominated by inaccurate dark current subtraction (taken from Chan et al. 2001, [20]).
\resizebox {11.5cm}{!}{\includegraphics{ChanSJ_3.eps}}

The discontinuities observed are still of unknown origin and may be either in ISO or in IRAS calibration. It is remarkable that the problem seems to be not related with inaccuracy at low flux levels induced by an inaccurate dark current subtraction since this would just increase the observed dispersion but it would not change the zero-point of the absolute flux calibration. Actually, the strongest discrepancies are observed in the group of the brightest sources.

Neither does the problem seem to be directly correlated with the inaccuracy of the diferent methods used for cirrus correction, since it equally affects sources with low and high background, as we have already mentioned.

An interesting independent comparison between ISO LWS and IRAS photometry at 60 and 100 $\mu $m was carried out by Brauher & Lord 2001, [12] on a large sample of extragalactic sources.

This sample consisted of observations of galaxies taken with the LWS in the grating modes (LWS01 and LWS02) that were reduced in a uniform manner using all of the advanced data reduction techniques of LIA and ISAP starting from OLP Version 7 data products. The galaxy sample comprised nearly all galaxies observed during the ISO mission whose far-infrared emission fell within the 75$^{\prime}$$^{\prime}$ LWS beam and had IRAS Point Source Catalogue detections. There were 155 such galaxies in the ISO Data Archive with 60 $\mu $m fluxes ranging from below 1 Jy to 300 Jy.

In this study, a small correction factor was introduced in the derivation of the ISO synthetic photometry at 60 $\mu $m with ISAP in order to account for the fraction of the IRAS 60 $\mu $m filter not covered by ISO LWS (27-87 $\mu $m is the spectral coverage of the IRAS 60 $\mu $m filter versus 43-197 $\mu $m for LWS). This may introduce some uncertainty in the derived values. Assuming that the majority of the galaxies used for this comparison span a narrow temperature range (30-45 K) the amount of the integrated flux measurement missed by LWS is estimated to vary from 2-8%. Thus, an average correction of 5% to the LWS 60 $\mu $m fluxes was applied to all the galaxies in the sample.

The LWS02 60 $\mu $m and 100 $\mu $m continuum fluxes must also have a secondary correction applied. The fluxes for this AOT were estimated by fitting a 2-5 $\mu $m linear baseline through the IRAS filter central wavelengths, essentially producing a monochromatic flux density. This flux density must be corrected to estimate the flux density IRAS found over its extended passband. Fitting a linear baseline to the spectra overestimates the integrated spectral photometry by 12% at 60 $\mu $m and 9% at 100 $\mu $m. Thus, the LWS02 fluxes were also corrected for these overestimations accordingly.

After these corrections were applied, the infrared sky background was estimated using IRSKY (images from the all-sky IRAS Survey Atlas with a resolution of 4$^{\prime}$ in each of the IRAS bands) and then removed from the LWS data, in a similar way as Method 2 described above does it. The background subtracted LWS data were then compared with the IRAS photometry at 60 and 100 $\mu $m quoted in the Point Source Catalogue.

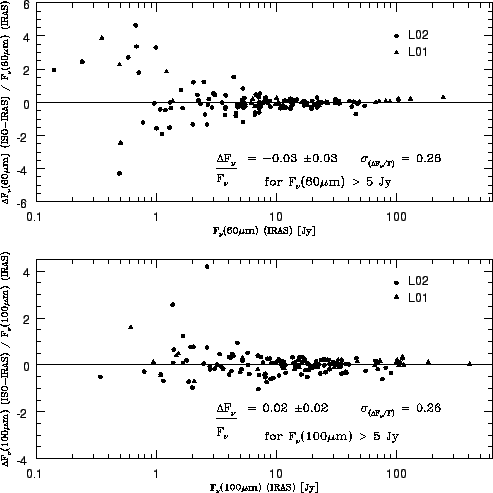
Figure 6.19 shows how the LWS and IRAS data compare after a careful reduction with the LWS Interactive Analysis software (LIA), including interactive dark currrent subtraction, absolute responsivity corrections, as well as manual removal of glitches and fringes.

Figure 6.19: The difference between the LWS and IRAS fluxes at 60 $\mu $m and 100 $\mu $m. The systematic offsets and dispersions of the LWS01 (triangles) and LWS02 (circles) data with respect to IRAS data are similar. The overall agreement is typically within 26% for fluxes above 5 Jy (from Brauher & Lord 2001, [12]).
\resizebox {12cm}{!}{\includegraphics{brauherj4.eps}}

Figure 6.20: LWS versus IRAS comparison for 60 $\mu $m and 100 $\mu $m. LWS01 observations are indicated with triangles while LWS02 observations are indicated with filled circles. The IRAS errors come from the Point Source Catalogue, and the ISO errors are a combination of the calibration and measurement uncertainty errors (from Brauher & Lord 2001, [12]).
\resizebox {11.5cm}{!}{\includegraphics{brauherj5.eps}}

The results obtained suggests an overall good agreement between ISO LWS and IRAS both at 60 and 100 $\mu $m, typically within 26% for fluxes above 5 Jy. The ISO fluxes, according to this study are (1) systematically lower than IRAS fluxes by 3% between 5-300 Jy at 60 $\mu $m and (2) systematically higher than the IRAS fluxes by 2% between 5-300 Jy at 100 $\mu $m. Below 5 Jy the dispersion increases by a factor of two and is attributed to the dark current subtraction errors.

However, it is worth to note that if only the brightest sources in the sample are considered (above 25 Jy) the LWS fluxes are found systematically 12% higher than the corresponding IRAS fluxes both at 60 $\mu $m and 100 $\mu $m. This result is strikingly similar to the offset found at 100 $\mu $m by Chan et al. 2001, [20].

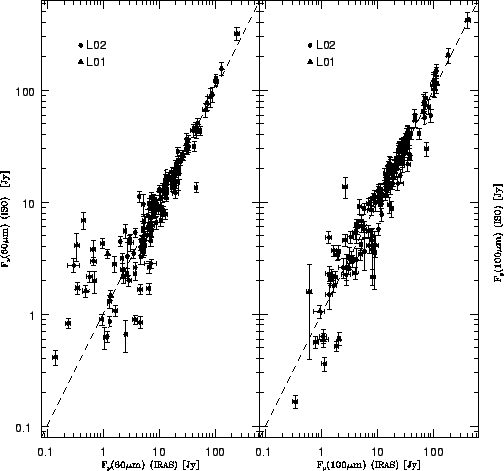
The strong discrepancies at high flux levels are more evident in Figure 6.20 where we have plotted the same results in a different format. The discrepancy seems to be of the order of 20-40% for fluxes above 70-80 Jy, supporting our previous findings.


6.3.1.3 ISO composite SWS+LWS spectra versus IRAS photometry at 60 and 100 $\mu $m

We can take advantage of the availability of the sample of cross-calibration sources used for the internal comparison between SWS and LWS presented in Section 6.2.1.4 to produce good quality, composite ISO SWS+LWS spectra which can be directly compared with IRAS photometry at 60 and 100 $\mu $m. The spectral coverage of the resulting ISO composite spectrum is such that there is no need need to apply in this case any correction factor to the IRAS photometry at 60 $\mu $m, since the IRAS photometric band is fully covered by ISO when we combine SWS+LWS data in a single spectrum.

The test sample includes 23 sources which are listed in Table 6.4. Note that, unfortunately, we had to exclude from this cross-calibration analysis some of the sources used in the previous comparison. For instance, this time we could not include the well known variable sources TX Cam or OH 26.5+0.6, observed close in time by ISO with SWS and LWS, but at a completely different epoch with respect to IRAS photometry, taken in 1983-1984. Neither we could use the source IRAS 15452$-$5459 because of the bad quality of its IRAS photometry at 60 and 100 $\mu $m.

Table 6.4: ISO OLP Version 10.1 synthetic photometry at 60 and 100 $\mu $m compared with IRAS photometry
IRAS IRAS IRAS ISO ISO IRAS
Source 60 $\mu $m 100 $\mu $m$^1$ 100 $\mu $m$^2$ 60 $\mu $m 100 $\mu $m CIRR2 Notes
HD 161796 151.7 48.7 49.2 167.3 56.3 1
NGC 6543 133.3 62.7 63.3 144.2 72.9 1
IRAS 19114+0002 515.9 168.1 169.8 674.5 224.3 1
R Dor 243.5 83.5 84.3 311.1 96.3 1 strong near infrared leak
CRL 618 1036 339.9 343.3 1361 547.4 1 bad SWS band 4
CPD $-$56 8032 199.1 91.7 93.5 236.5 105.0 2
CW Leo 5652 922.0 940.0 5297 1247 2
Circinus 248.7 315.9 322.2 314.6 426.3 2 bad SWS band 4
HD 101584 193.0 104.0 110.2 226.4 132.5 3
Hen 2$-$113 176.6 71.3 75.6 217.5 94.7 3
M 1$-$78 589.6 408.2 432.7 792.6 592.6 3
HD 44179 173.1 66.2 70.2 215.1 81.9 3
IC 418 103.6 31.2 33.1 119.6 35.4 3
IRAS 16342$-$3814 290.2 139.4 157.5 262.8 122.1 4 mean of two measurements
SAO 34504 96.6 41.0 46.3 119.1 44.0 4 bad SWS band 4
AFGL 4106 851.8 181.1 239.1 1053 310.4 5
$\mu $ Cep 127.0 49.9 65.9 140.1 52.8 5 strong near infrared leak
IRAS 16594$-$4656 131.4 34.4 61.2 146.2 78.2 6
IRAS 21282+5050 33.4 15.0 26.7 38.6 31.4 6
IRAS 21318+5631 90.0 25.4 44.7 93.8 45.0 6
$\alpha $ Sco 115.5 31.9 56.1 139.2 53.2 6 bad SWS band 4
& strong near infrared leak
VX Sgr 262.7 82.3 144.9 312.9 197.9 7

$^1$ IRAS flux density quoted in the Point Source Catalogue
$^2$ restored IRAS flux density including background cirrus emission

At these long wavelengths, and as it was already mentioned in Section 6.3.1.2, one needs to consider very seriously the amount of cirrus contamination in the measurements. In principle, the effect is expected to be strong only at 100 $\mu $m in regions of strong cirrus background while the measurements at 60 $\mu $m will only be slightly affected. In any case, in order to take this possibility into account and because it can be of help in the analysis, the sources in Table 6.4 have been sorted as a function of the parameter CIRR2, previously defined in Equation 6.1, which is directly related with the background emission at 100 $\mu $m in the vicinities of the IRAS point source.

For the derivation of the ISO SWS+LWS synthetic photometry at 60 and 100 $\mu $m listed in Table 6.4 we used again ISAP Version 2.1. First the corresponding SWS+LWS OLP Version 10.1 spectra were directly retrieved from the ISO Data Archive and combined to create the composite spectra. Then bad data points affected by glitches in both SWS and LWS sections of the composite spectra were removed and the LWS spectra were corrected for near infrared leaks when necessary. Finally the syn_phot application of ISAP was used to convolve the ISO spectrum with the transmission profile of the IRAS filters at 60 and 100 $\mu $m. This way we derived a monochromatic flux at each of these wavelengths under the assumption that the source SED shape is of the form $\nu$ $\times$ f$_{\nu}$ = constant, or equivalently $\lambda$ $\times$ f$_{\lambda}$ = constant, in the same way as IRAS did.

Figure 6.21 shows the distribution of the derived ISO/IRAS flux density ratios at 60 $\mu $m as a function of the IRAS flux density at 60 $\mu $m in logarithmic scale. As we can see the systematic discrepancy between ISO and IRAS photometry at 60 $\mu $m (of the order of 15%) is confirmed.

The discrepancy cannot be attributed to background contamination since it is not correlated at all with the value of the IRAS CIRR2 parameter. Instead, there seems to be a clear correlation with increasing flux, similar to that previously found for the sample of extragalactic sources analysed in Section 6.3.1.2.

In order to determine whether this systematic discrepancy between ISO and LWS is also found at 100 $\mu $m we used again the sources in Table 6.4 to perform an independent analysis.

Figure 6.21: The ISO/IRAS flux density ratios at 60 $\mu $ as a function of the IRAS flux density at 60 $\mu $m.
\resizebox {7.6cm}{!}{\includegraphics{iso60_iras60.ps}}

Following the strategy proposed by Josephine Chan in their comparison of ISO data with IRAS photometry at 100 $\mu $m, we used their Method 1, this is, the restoration of the background emission estimated from the CIRR2 parameter to the quoted IRAS flux density at 100 $\mu $m in the IRAS Point Source Catalogue Version 2.1, to determine the total cirrus+source flux density. This is the quantity that must be used to compare with the LWS measurements, as LWS measured both source+background emission.

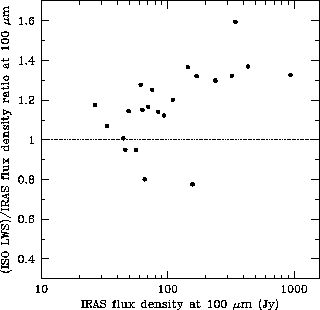
Figure 6.22 shows in logarithmic scale the distribution of ISO/IRAS flux density ratios at 100 $\mu $m as a function of the restored IRAS flux density at 100 $\mu $m.

Figure 6.22: The ISO/IRAS flux density ratios at 100 $\mu $ as a function of the restored IRAS flux density at 100 $\mu $m for the same calibration sample used in Figure 6.21.
\resizebox {7.6cm}{!}{\includegraphics{iso100_iras100.ps}}

Interestingly, we see again the same effect. ISO equivalent fluxes at 100 $\mu $m are found to be around 20% higher if we take the mean value of all measurements and up to 60% in the most extreme cases. The discrepancies found are not correlated with IRAS CIRR2, being equally distributed among sources with low and high background contamination. Surprisingly we find again, instead, what seems to be a clear correlation with the flux level, so that in general the brightest sources are those showing the strongest discrepancies while ISO data and IRAS photometry appear consistent to within the 25% level for sources below 100 Jy.

A plot which combines all the results obtained in the three independent cross-calibration analysis performed at 60 and 100 $\mu $m between ISO and IRAS here presented is shown in Figure 5.8 of the ISO Handbook Volume III on LWS.

In summary, our conclusion is that both at 60 and 100 $\mu $m IRAS and ISO agree within a few % in average for sources fainter than 25 Jy, while ISO fluxes are found systematically higher than IRAS fluxes for sources brighter than 25 Jy. The difference increases from about 15% around 100 Jy, to a level of about 20% for sources up to 400 Jy, and up to 30-50% for sources brighter than 400 Jy.

The reason for this behaviour is not understood. We know it is not due to inaccurate dark current subtraction, nor to cirrus background contamination. A possible cause could be some non-linearities in the infrared detectors. However, the problem could be associated with IRAS data and not with ISO.

Indeed, Figure IV.A.4.2 of the IRAS Explanatory Supplement, [84] does evidence detector non-linearity behaviour and Section VI.B.4.d quotes errors of respectively 30% and 70% at 60 and 100 $\mu $m for sources above 100 Jy.


6.3.1.4 LWS raster scans of extended sources versus IRAS photometry

LWS observations have also been made at a number of positions in the complex Trumpler 14 and 16 fields, and in the direction of the Galactic Centre. LWS data have been compared with the IRAS 100 $\mu $m fluxes at the same positions. All fields contain large areas of extended emission, which although relatively smooth, do change by a factor of $\sim$40 within each region.

The point source fluxes (Jy) provided by the LWS pipeline calibration have been converted to extended source fluxes (MJy sr$^{-1}$) using the correction factors implemented in ISAP Version 2.0.

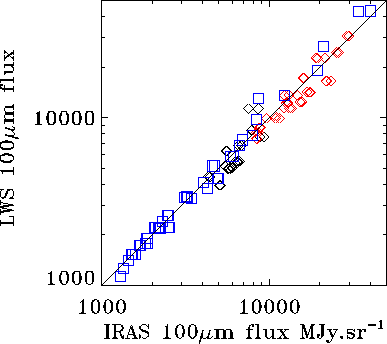
Figure 6.23 shows the comparison of the converted LWS and IRAS 100 $\mu $m fluxes. As we can see, the results indicate that there is an excellent agreement between the fluxes provided by ISO and the IRAS results. From the analysis of the data we obtain a mean ratio, LWS/IRAS = 1.0$\pm$0.1.

Figure 6.23: Comparison of LWS and IRAS 100 $\mu $m fluxes in the Trumpler 14 (red diamonds), Trumpler 16 (black diamonds), and Galactic Centre (blue squares) fields.
\resizebox {10cm}{10cm}{\includegraphics{all100uLWS-IRAS.eps}}

Part of the uncertainty is probably due to the unresolved structure of the sources observed within the beam. This is because the extended source correction factors applied have been derived under the assumption of a smooth and very extended flux distribution. In the real world, structure or embedded sources could produce significant discrepancies from the ideal situation and, with it, differences in flux.

Note also that for fields containing multiple sources the observed flux will depend critically on the precise positions of the sources relative to the optical axis. To recover or model the observed flux requires positional information on the sources and a deconvolution with the PSF and instrumental profile. Indeed, for single point sources observed off-axis a similar procedure is required to recover the correct flux.


6.3.1.5 ISOPHOT-P and -C versus IRAS photometry

The database of ISO observations generated by a project intended to search for Vega-like debris disks around nearby main-sequence stars (Habing et al. 1996, [69]; Laureijs et al. 2002, [106]) has also been used to assess the quality of ISOPHOT photometric calibration.

The sample contains more than 80 main sequence stars that were observed with ISOPHOT at 25, 60, 150 and 170 $\mu $m, in order to determine whether the star had an infrared excess indicating the presence of a dusty disk. Unfortunately, the number of stars found with disks was very low: only 8 out of 65 stars observed with ISO showed a significant excess at 60 $\mu $m.

The positive point, from the cross-calibration perspective, is that the non-detected stars constitute a nice homogeneous sample of observations which can be used to improve our knowledge of the quality of the observations made with ISOPHOT by comparing the observations with models and with the IRAS photometry of the same sources at 25 and at 60 $\mu $m.

The subsample of observations here analysed were performed using the AOT PHT03 (PHT-P detectors) in triangular chopped mode at 25 $\mu $m and mini-maps (3$\times$3 with 46$^{\prime}$$^{\prime}$ steps) centred at the source location at 60 $\mu $m using the AOT PHT22, and reflects the status of the PHT calibration as of OLP Version 8.

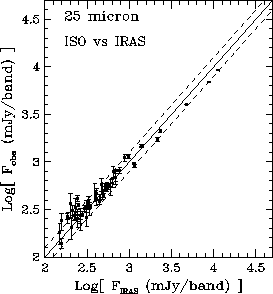
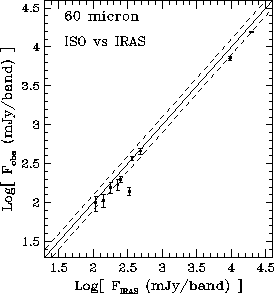
Figure 6.24 shows the result of the ISO observations compared to the IRAS photometry (when available) of the stars observed at 25 and 60 $\mu $m.

Figure 6.24: The flux densities of the 80 main sequence stars included in the Vega project derived from ISO chopped PHT-P photometry at 25 $\mu $m (left) and PHT-C mini-maps at 60 $\mu $m (right) are compared to IRAS photometry. (from Laureijs et al. 1999, [105]).
\resizebox {6.2cm}{!}{\includegraphics{p25iso_vs_iras.eps}} \resizebox {6.2cm}{!}{\includegraphics{c100iso_vs_iras.eps}}

As we can see, the level of agreement with IRAS photometry at 25 $\mu $m is in most cases better than 25%. The brighter targets (F$_{25}$ $>$ 1 Jy) appear to have systematically ISO flux densities lower than the IRAS values. This underestimation is expected from the usage of the chopped mode, where a relatively high source-background contrast causes a signal loss due to transient responsivity in the PHT-P detector. On the other hand, the ISO fluxes of the fainter stars (F$_{25}$ $<$ 300 mJy) appear overestimated with respect to IRAS. The explanation for this overestimation is still not clear but it might be the result of (i) the peculiar transient behaviour of the P2 detector, (2) a low level signal non-linearity, or (3) uncertainties in the IRAS calibration (we have to consider that at these low flux levels we are close to the detection limit of IRAS at 25 $\mu $m).

At 60 $\mu $m the statistics become poorer. IRAS fluxes are available only for 11 targets. The obvious outlier showing F$_{60,IRAS}$ $>>$ F$_{60,ISO}$ consists of 3 resolved point sources in the ISOPHOT map. For the remaining detections the correlation is high. However, the ISO observations are systematically ($\sim$25%) below the IRAS values. This discrepancy could partially be attributed to the fact that we have assumed point source calibration in the conversion from measured flux in an array pixel to the final target flux. In case of small extended sources the flux would be underestimated for this reason and this is actually what we observe in stars like Vega and $\beta $-Pictoris, contained in the sample, which are known to be slightly extended infrared sources.

As a consequence of the calibration upgrades implemented in the latest versions of the ISOPHOT pipeline, the accuracy of chopped PHT-P and PHT-C photometry has further improved significantly.

As an example, we show in Tables 6.5 and 6.6 the photometric data derived from OLP Version 10 for a subset of the stars in the sample above mentioned compared with IRAS photometry and model predictions (Ulrich Klaas, private communication). ISOPHOT and IRAS fluxes are colour corrected.


Table 6.5: OLP Version 10 chopped PHT-P photometry at 25 $\mu $m compared to IRAS photometry and model predictions
Source ISOPHOT flux IRAS flux Model flux
$[Jy]$ $[Jy]$ $[Jy]$ $[Jy]$
Sirius 18.52 24.09 21.54
HR7557 5.24 5.76 5.27
HR7310 4.31 3.66 3.40
HR5986 0.68 0.53 0.52
0.63
0.58
HR5914 0.39 0.41 0.38
HR5447 0.32 0.30 0.26
HR7469 0.25 0.22 0.25

Table 6.6: OLP Version 10 chopped PHT-C photometry at 60 $\mu $m compared to IRAS photometry and model predictions
Source ISOPHOT flux IRAS flux Model flux
$[Jy]$ $[Jy]$ $[Jy]$ $[Jy]$
Sirius 4.08 3.73 3.68
4.04
HR1654 1.68 1.53 1.61
HR7980 1.25 1.12 1.17
HR7557 0.95 0.95 0.90
HD185144 0.11 0.12 0.10
HR7469 0.06 <0.75 0.04


6.3.2 Comparison with MSX

In order to extend the cross-calibration analysis of ISO SWS to observations made with other space facilities than IRAS we performed a similar analysis using this time photometric data provided by the Midcourse Space Experiment (MSX; Egan et al. 1999, [48]).

Briefly, MSX was a multi-discipline experiment sponsored by the USA Ballistic Missile Defense Organization. The principal objective of the MSX astronomy experiments was to complete the census of the mid-infrared sky. Experiments were designed to cover the regions either missed by IRAS and COBE/DIRBE or where the sensitivity of IRAS was degraded by confusion noise in regions of high source densities or structured extended emission, including the entire Galactic Plane.

The MSX Point Source Catalogue contains all the point sources detected with signal-to-noise ratio $>$ 3 following criteria very similar to IRAS (detection requires multiple confirmations).

The infrared instrument on MSX was a 35 cm clear aperture off-axis telescope cooled by a single solid H$_2$ cryostat equipped with Si:As BiB arrays with eight columns of detectors, each with 192 rows of 18''.3 square pixels, and a high sensitivity (0.1 Jy at 8.3 $\mu $m). Two narrow band filters covered the spectral regions centred at 4.29 (B1) and 4.35 (B2) $\mu $m, and four broad-band filters covered the spectral regions centred at 8.28 (A), 12.13 (C), 14.65 (D) and 21.34 (E) $\mu $m (see Table 6.7).

Table 6.7: Description of MSX photometric bands
Band No Isophotal 50% Isophotal Zero Abs. Survey Effective FOV
active $\lambda$[$\mu $m] peak BW[$\mu $m] mag. photom. sens. $\Omega_{EFOV}$
cols. intensity flux [Jy] accuracy [Jy] [$\times$10$^{-9}$sr]
A 8 8.28 6.8$-$10.8 3.36 58.49 5% 0.1$-$0.2 10.6
B$_1$ 2 4.29 4.22$-$4.36 0.104 194.6 9% 10$-$30 14.0
B$_2$ 2 4.35 4.24$-$4.45 0.179 188.8 9% 6$-$18 14.0
C 4 12.13 11.1$-$13.2 1.72 26.51 3% 1.1$-$3.1 11.7
D 4 14.65 13.5$-$15.9 2.23 18.29 4% 0.9$-$2 11.3
E 2 21.34 18.2$-$25.1 6.24 8.80 6% 2$-$6 12.6

In the following analysis we will only consider the broad MSX filters A, C, D and E, which are the most sensitive filters onboard MSX.

About 100 sources with an available SWS01 spectrum in the ISO Data Archive were identified to have their corresponding mid-infrared counterpart in the MSX Point Source Catalogue.

After excluding from this sample all the suspected variable stars and extended sources (as we did for the cross-calibration with IRAS) we ended up with around 50 sources suitable for cross-calibration with MSX at all the above mentioned filters.

The OLP Version 10 SWS spectra of these sources were retrieved from the ISO Data Archive and further processed with ISAP Version 2.1. Bad data points affected by glitches were identified and removed from the SWS spectra using the available tools in ISAP and ISO `synthetic photometry' was performed at the A, C, D and E MSX filters with the help of syn_phot. This ISAP application convolves the ISO spectrum with the transmission profile of the corresponding MSX filters assigning a monochromatic flux to each band under the assumption that the SED shape is of the form $\nu$ $\times$ f$_{\nu}$ = constant, or equivalently $\lambda$ $\times$ f$_{\lambda}$ = constant.

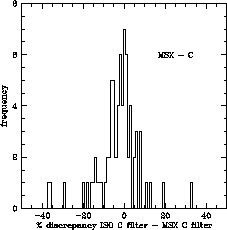
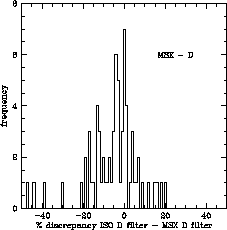
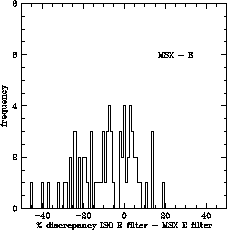
In Figures 6.25 to 6.28 we show the results obtained. As we can see, they are very similar to the ones obtained in the previous cross-calibration comparison with IRAS data.

Figure 6.25: ISO SWS synthetic photometry at 8.28 $\mu $m derived from OLP Version 10 data products compared to MSX filter A photometry at the same wavelength. The dashed red line represents a 15% discrepancy level.
\resizebox {15cm}{!}{\includegraphics{msx_A_sws_olp10.ps}}

Esentially, the absolute flux calibration of ISO SWS and MSX agrees to within the 10-15% level at all flux levels, with very little degradation even at the lower flux levels.

The few outliers are interpreted as previously unknown variable sources and/or slightly badly pointed observations, similarly to what was observed in the previous comparison with IRAS.

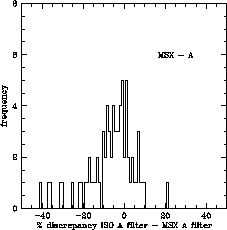
Comparing the absolute flux level of all the measurements peformed with ISO and MSX there is a general good agreement in all filters with a zero-point consistency better than 5% in all cases with the exception of filter A (see Figure 6.29), where the distribution of observed discrepancies show a marked asymmetry.

Figure 6.26: ISO SWS synthetic photometry at 12.13 $\mu $m derived from OLP Version 10 data products compared to MSX filter C photometry at the same wavelength. The dashed red line represents a 15% discrepancy level.
\resizebox {15cm}{!}{\includegraphics{msx_C_sws_olp10.ps}}

This asymmetry is most probably due to a higher percentage of badly pointed observations (similarly to what we observed also in the cross-calibration comparison with IRAS at 12 $\mu $m). Note that this is the filter covering a wavelength range where SWS is most sensitive to small pointing offsets because of the smaller aperture size.

On the other hand, the slightly worse correlation found between ISO SWS and MSX filters D and E (compared to filters A and C) is probably induced by the fact that these filters show a larger overlap with SWS band 3, which is known to be less accurate than SWS band 2 in terms of absolute flux calibration.

Figure 6.27: ISO SWS synthetic photometry at 14.65 $\mu $m derived from OLP v10 data products compared to MSX filter D photometry at the same wavelength. The dashed red line represents a 15% discrepancy level.
\resizebox {15cm}{!}{\includegraphics{msx_D_sws_olp10.ps}}

Figure 6.28: ISO SWS synthetic photometry at 21.34 $\mu $m derived from OLP v10 data products compared to MSX filter E photometry at the same wavelength. The dashed red line represents a 15% discrepancy level.
\resizebox {14.2cm}{!}{\includegraphics{msx_E_sws_olp10.ps}}

Globally considered, the main difference found with respect to the previous cross-calibration comparison with IRAS is the absence of the strong discrepancies observed at high flux levels between ISO and IRAS data. This supports our hypothesis that the non-linearity problem is in the IRAS calibration at high flux levels.

Figure 6.29: Distribution of discrepancies found between the ISO SWS synthetic photometry at 8.28, 12.13, 14.65 and 21.34 $\mu $m, derived from OLP Version 10 data products compared to MSX filter A, C, D and E photometry, respectively.
\resizebox {5.4cm}{!}{\includegraphics{stat_A.ps}} \resizebox {5.4cm}{!}{\includegraphics{stat_C.ps}}
\resizebox {5.4cm}{!}{\includegraphics{stat_D.ps}} \resizebox {5.4cm}{!}{\includegraphics{stat_E.ps}}


6.3.3 Comparison with COBE/DIRBE

ISOPHOT data has also been compared with COBE/DIRBE data as part of our cross-calibration analysis. The Diffuse Infrared Background Experiment (DIRBE; Hauser et al. 1998b, [76]) was one of the three instruments onboard COBE (the Cosmic Background Explorer), a satellite developed by NASA's Goddard Space Flight Center and launched in November 1989 to measure the diffuse infrared and microwave radiation from the early universe to the limits set by our astrophysical environment.

DIRBE obtained infrared absolute sky brightness maps in the wavelength range 1.25 to 240 $\mu $m. Most of this range was also covered by ISOPHOT. However, the comparison between ISOPHOT and COBE/DIRBE data is complicated, mainly because of the vastly different beam sizes (42$^{\prime}$ FWHM for COBE/DIRBE), as we will see below.


6.3.3.1 PHT-S spectroscopy versus COBE/DIRBE photometry

In order to check the consistency between the absolute flux calibration of COBE/DIRBE photometry and PHT-S spectroscopy we present here a comparison of the absolute surface brightness of the zodiacal light measured by PHT-S and COBE/DIRBE data reported by Dotto et al. 2002, [46].

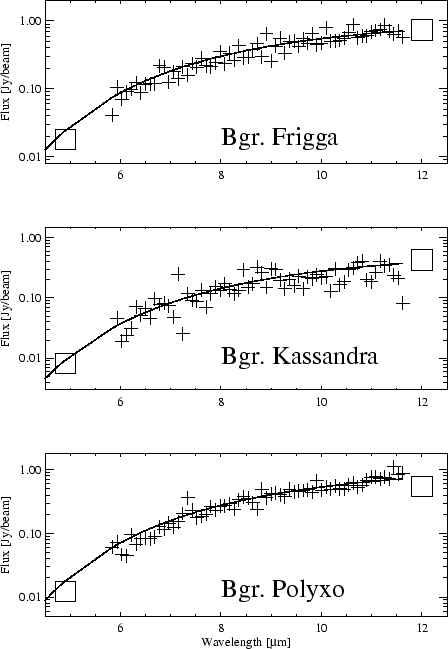
Figure 6.30 shows the OLP Version 9.0 sky background measurements taken with the long wavelength channel of PHT-S in the vicinities of the asteroids Frigga, Kassandra and Polyxo together with COBE data at 4.9 and 12 $\mu $m. Note that the zodiacal light is the dominating background at the PHT-S wavelengths.

Figure 6.30: Comparison of PHT-S sky background measurements made in the vicinities of the asteroids Frigga, Kassandra and Polyxo (crosses) with COBE data at 4.9 and 12 $\mu $m (squares). The solid line corresponds to the fitted blackbody curve (from Dotto et al. 2002, [46]).
\resizebox {12cm}{!}{\includegraphics{phts_bgr.ps}}

As we can see PHT-S is in excellent agreement with COBE data. From the sky background observed we can deduce that the zodiacal light can be well approximated by a blackbody emitting at a temperature of 267 K.

For the short wavelength channel the comparison is not possible because the extremely low flux in this range is below the detection limit of PHT-S. In spite of this we see that the featureless PHT-S spectrum fits nicely between the COBE/DIRBE photometric data points at 4.9 and 12 $\mu $m.

Unfortunately, COBE did not cover wavelengths in between 5 and 12 $\mu $m, in the range where the brightness of the zodiacal light rises very steeply. However, complementary results obtained with PHT-P and ISOCAM confirm that the zodiacal emission spectrum can be well fitted by a blackbody of 267 K and that the spectrum is featureless between 5 and 16 $\mu $m.


6.3.3.2 PHT-C versus COBE/DIRBE photometry

The consistency of the absolute sky brightness derived from ISO C100 maps with COBE/DIRBE data was also verified as part of the OLP Version 8.4 scientific validation of PHT22 staring raster maps (Klaas et al. 2000, [100]).

The mean surface brightness of specific areas of the sky was derived from the full C100 maps used for the flat-field assessment and compared with the surface brightness values in the corresponding filters or adjacent filters of COBE/DIRBE. The use of the full area of the ISOPHOT maps offers the advantage of getting a solid angle coverage comparable to the COBE/DIRBE pixels. However, in most cases the solid angles of the ISOPHOT maps are still considerably smaller than one pixel in COBE/DIRBE. The COBE/DIRBE annual maps were used (since at the wavelengths considered the contribution from the zodiacal light is very small) to determine the fluxes for the DIRBE pixel coincident with the map area centroid. For a check of the large scale variations of the sky background average fluxes of a 1.5 degree circular area were as well determined. ISOPHOT maps containing bright sources were not considered (they would give a considerably higher average surface brightness due to the smaller area considered).

In Table 6.8 we present the results obtained. Except for the different beam sizes a comparison of the ISOPHOT/DIRBE 60 and 100 $\mu $m filters is relatively straightforward. In general a good agreement better than 25%, in particular for those maps with comparable sizes to the COBE/DIRBE beam, is found. All larger deviations can be explained by the source structure which is extended over the ISOPHOT map area, but compact inside the COBE/DIRBE beam. The largest outlier shows a similar excess in the C200 range.

Without any correction, the ISOPHOT 90 $\mu $m filter maps seem to show a systematic positive surface brightness excess with regard to the DIRBE 100 $\mu $m photometry. However, inspection of the COBE/DIRBE SEDs indicates a steep decline in flux between 60 and 100 $\mu $m. In fact, the 90 $\mu $m ISOPHOT values are practically always in between the 60 and 100 $\mu $m DIRBE values. Very often, the surface brightness ratio 60/100 is about 2, i.e. with a linear interpolation between 60 and 100 $\mu $m, the 90 $\mu $m flux is by 25% higher than the 100 $\mu $m flux due to the shape of the SED. Then, also the surface brightness of the 90 $\mu $m maps are consistent with COBE/DIRBE within the 25% level. If the discrepancy between the ISOPHOT 90 $\mu $m surface brightness and the DIRBE 100 $\mu $m surface brightness is small, usually the source SED is reasonably flat between 60 and 100 $\mu $m. Whether there is still a positive excess at 90 $\mu $m cannot be solved by this kind of study, but needs better matching areas and a proper colour correction of the background SEDs.

From the consistency found in the three filters at 60, 90 and 100 $\mu $m and the relative photometric accuracies of all ISOPHOT C100 filters, we conclude that the consistency should also hold for the remaining ISOPHOT filters at 65, 80 and 105 $\mu $m. The good correspondance holds for the flux range 4.5 to 400 MJy sr$^{-1}$.

Table 6.8: Consistency check of C100 map absolute surface brightness with COBE/DIRBE annual map photometry. The solid angle of one COBE/DIRBE pixel is 19.5 10$^{-5}$ sr. No correction for the wavelength shift between ISOPHOT 90 $\mu $m and DIRBE 100 $\mu $m filters has been performed which causes for most sky backgrounds a systematic positive excess of the 90 $\mu $m flux (see text for details).

OLP 		surface solid DIRBE DIRBE solid
product filter brightness angle flux filter angle consistency
name [$\mu $m] [MJy sr$^{-1}$] [10$^{-5}$sr] [MJy sr$^{-1}$] [$\mu $m] [10$^{-5}$sr] [%]
19002101 60 6.8 0.81 6.6 60 19.5 +2.2
08900102 60 9.5 1.60 6.5 60 19.5 +47
85001219 60 22.8 0.21 22.3 60 19.5 +2.2
13400214 60 39.8 0.22 39.6 60 19.5 +0.6
68300807 60 21.3 6.77 27.2 60 19.5 $-$22
84403913 60 23.9 1.04 24.5 60 19.5 $-$2.5
69801101 60 107.4 1.16 122.3 60 19.5 $-$12
35100809 90 5.1 5.49 3.3 100 19.5 +55
58200903 90 11.8 3.06 12.9 100 19.5 $-$7.9
19201091 90 4.8 7.30 3.1 100 19.5 +52
86901244 90 5.2 2.75 3.6 100 19.5 +44
41502788 90 8.1 5.10 5.7 100 19.5 +44
09000606 90 11.8 0.77 11.3 100 19.5 +4.4
08901904 90 15.1 0.23 13.6 100 19.5 +11
40100614 90 14.7 6.80 13.3 100 19.5 +10
87001338 90 5.3 2.93 3.6 100 19.5 +47
57501902 90 12.1 1.15 9.7 100 19.5 +25
53700514 90 4.4 0.85 3.7 100 19.5 +21
60002009 90 7.1 4.24 5.2 100 19.5 +37
50000124 90 4.8 8.87 3.3 100 19.5 +43
50100273 90 5.8 8.68 3.5 100 19.5 +68
20701079 90 25.6 0.33 22.8 100 19.5 +12
20800709 90 5.8 3.49 4.0 100 19.5 +46
86800640 90 5.7 2.96 3.6 100 19.5 +60
10101158 100 30.7 1.71 21.0 100 19.5 +46
79401149 100 44.2 0.51 40.6 100 19.5 +9.0
44900714 100 387.7 15.2 440.1 100 19.5 -12
15601578 100 17.4 1.82 6.1 100 19.5 +187
27600420 100 15.4 1.74 12.1 100 19.5 +27
71901220 100 18.5 3.66 16.0 100 19.5 +15
33401134 100 96.4 4.06 49.3 100 19.5 +96

A similar analysis was also performed by Klaas et al. 2000, [100] for ISOPHOT C200 maps. Since the longest COBE/DIRBE filters (140 and 240 $\mu $m) have an internal uncertainty of 20 to 30%, for a subsample of maps with low dynamic range the average fluxes of a 1.5 degree circular area were used, which gives a more robust photometry (this means averaging over 70 COBE/DIRBE pixels).

In Table 6.9 we present the results of the comparison. No colour correction with regard to a modified blackbody describing the background spectral energy distribution nor a wavelength correction to better match the COBE/DIRBE filter central wavelength with the ISOPHOT filter central wavelength were performed. Again we have to remark that nearly all the ISOPHOT maps are considerably smaller in area than the solid angle of one COBE/DIRBE pixel. Therefore, structures in the source or background can affect the resulting absolute flux. In case of a flat field, the flux of the centred COBE/DIRBE pixel as well as the 3 degree circular area average is listed to give an impression of the variation of the background (and also the stability of the COBE/DIRBE measurement in one pixel). If the map contains a bright target and is smaller than the COBE/DIRBE pixel, then only the flux of the centred COBE/DIRBE pixel is given.

Taking into account the discrepancies in beam size and the non-correction for different wavelengths of filters and background SEDs, the general agreement is in the order of 20 to 30% at all four filters considered (150, 170, 180 and 200 $\mu $m). Restricting the comparison to ISOPHOT maps with comparable solid angles with the COBE/DIRBE measurement, the consistency is confirmed to be better than 25%. This holds for all filters and a surface brightness range between 2.5 and 600 MJy sr$^{-1}$.

Larger deviations between the average ISOPHOT map flux and the COBE/ DIRBE flux only occur for bright central sources which are compact in comparison with the COBE/DIRBE beam. In these cases, the COBE/DIRBE fluxes are always less than the ISOPHOT fluxes, as expected.

Table 6.9: Consistency check of C200 map absolute surface brightness with COBE/DIRBE annual map photometry. The solid angle of one COBE/DIRBE pixel is 19.5 10$^{-5}$ sr (see text for details).
surface solid DIRBE DIRBE solid
OLP product filter brightness angle flux filter angle consistency
name [$\mu $m] [MJy sr$^{-1}$] [10$^{-5}$sr] [MJy sr$^{-1}]$ [$\mu $m] [10$^{-5}$sr] [%]
56200110 150 3.6 2.91 4.1 140 19.5 $-$13
56201814 150 22.2 0.42 20.9 140 19.5 +6.2
08900103 150 5.5 1.26 7.7 140 19.5 $-$29
79400434 170 3.2 3.15 2.2 140 19.5 +45
2.9 140 215.3 +10
59300101 170 3.5 6.53 3.5 140 19.5 $-$1.4
3.4 140 215.3 +4.2
19800208 170 3.2 3.41 5.0 140 19.5 $-$37
3.3 140 215.3 $-$3.6
21001305 170 3.6 3.39 4.1 140 19.5 $-$12
3.5 140 215.3 +3.4
79900733 170 6.0 0.50 7.0 140 19.5 $-$14
33600108 180 2.7 2.50 2.7 140 19.5 $-$2.6
2.8 140 215.3 $-$4.0
33600705 180 4.7 2.55 5.7 140 19.5 $-$17
5.7 140 215.3 $-$17
35100907 180 4.1 4.92 4.5 140 19.5 $-$8.2
16701206 180 15.0 4.11 12.7 140 19.5 +18
52700412 180 3.2 0.87 3.8 140 19.5 $-$16
3.2 140 215.3 +0
85001037 180 8.1 3.78 10.1 140 19.5 $-$19
9.3 140 215.3 $-$13
78200101 200 6.3 28.40 5.3 240 34.45 +20
36803005 200 14.8 0.71 15.5 240 19.5 $-$4.5
14.9 240 215.3 $-$0.9
39602213 200 36.2 6.22 29.2 240 19.5 +24
26101401 200 69.8 11.03 85.4 240 19.5 $-$18
33401133 200 138.6 3.89 87.6 240 19.5 +58
86101801 200 251.9 5.01 287.9 240 19.5 $-$13
15601577 200 11.4 1.38 5.9 240 19.5 +95
33300559 200 38.0 6.55 55.7 240 19.5 $-$32
10101157 200 69.7 1.41 45.2 240 19.5 +54
31000625 200 345.4 1.45 207.8 240 19.5 +66
26701013 200 593.3 15.49 494.5 240 19.5 +20
40900802 200 6.9 1.97 5.6 240 19.5 +23
28001303 200 13.0 2.00 12.8 240 19.5 +1.6

next up previous contents index
Next: 6.4 Comparison with Models Up: 6. ISO Cross-Calibration Previous: 6.2 Internal Cross-Calibration
ISO Handbook Volume I (GEN), Version 2.0, SAI/2000-035/Dc