Some explanation of how the pointing (as given in the IIPH and other similar files) is calculated is presented here.

The attitude of a satellite is usually expressed by astronomers (and by FITS standard) in terms of the 3 angles:

and

, that specify the orientation of the instrument in the inertial J2000 frame.

and

are the usual astronomical equatorial coordinates specified in degrees, while

is the angle, measured anticlockwise, between north and the spacecraft z-axis (see Figure 3.2). This uses the normal astronomical definition of East (to the left).

Operationally, on the other hand, attitudes are specified in terms of 4-component `quaternions':

that provide the most concise representation of the series of rotations that are required to specify the satellite attitude. For a rotation of D degrees about an axis specified by the direction cosines

the quaternion components are given by

The resultant quaternion, $Q_{ab}$ , of successive rotations

and

is the product of a $4\times 4$ matrix, each of whose elements is one of the elements of

, and the $4\times 1$ matrix representation of

, i.e.:

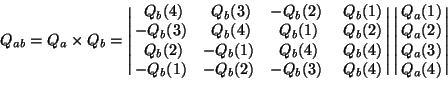$\begin{displaymath} Q_{ab} = Q_a \times Q_b = \left\vert \matrix{ \ Q_b(4) & ... ..._a(1) \cr Q_a(2) \cr Q_a(3) \cr Q_a(4) } \right\vert \bigskip\end{displaymath}$

(F.6)

The Attitude and Orbit Control System (AOCS) delivers instantaneous estimates of the Star-Tracker quaternions

that define the STR J2000 pointing. These have to be combined with the STR/QSS misalignment quaternions

and with any of the QSS/Instrument alignment quaternions (one per aperture):

[ $\times$ any raster point quaternion

] to give a resultant quaternion,

, that defines the orientation of an instrument in the inertial frame.

$\begin{displaymath} (CAM) Q = [RPQ\times ] QSSCAMQ \times STRQSSQ \times STRQ \end{displaymath}$

(F.7)

defines the orientation of the (CAM) x-, y- and z-instrument axes. If

and

are the instrument axis unit vectors in the J2000 inertial frame, then:

$\displaystyle <X> = (Instrument) Pointing direction$
$\displaystyle = (RA,DEC)$			(F.8)
$\displaystyle <Y> = (Instrument) y-axis$			(F.9)
$\displaystyle <Z> = (Instrument) z-axis$			(F.10)

$\displaystyle <X> = cos(DEC)cos(RA)<i> + cos(DEC)sin(RA)<j> + sin(DEC)*<k>$			(F.11)
$\displaystyle sin(DEC) = 2(Q(1)Q(3)-Q(2)*Q(4))$			(F.12)
$\displaystyle cos(RA)cos(DEC) = Q(1)Q(1)-Q(2)Q(2)-Q(3)Q(3)+Q(4)*Q(4)$			(F.13)
$\displaystyle sin(RA)cos(DEC) = 2(Q(1)Q(2)+Q(3)Q(4))$			(F.14)
$\displaystyle cos(ROLL)cos(DEC) = -Q(1)Q(1)-Q(2)Q(2)+Q(3)Q(3)+Q(4)*Q(4)$			(F.15)
$\displaystyle sin(ROLL)cos(DEC) = 2(Q(1)Q(4)+Q(2)Q(3))$			(F.16)

These instantaneous attitude estimates are given in the IIPH columns XRA, XDEC and XROLL.

F. Quaternions