The resolving
power for the grating-only mode was typically ![]() 200. To
enhance this, Fabry-Pérot (FP) etalons were used to further select only a
narrow portion of the spectrum within the grating passband. Although
inherently capable of very high resolving power
200. To
enhance this, Fabry-Pérot (FP) etalons were used to further select only a
narrow portion of the spectrum within the grating passband. Although
inherently capable of very high resolving power ![]() the FP
interferometers, as used in ISO, were limited by the grating
performance (see Figure 2.5) and by the ohmic losses in
the FP plates, as discussed below.
the FP
interferometers, as used in ISO, were limited by the grating
performance (see Figure 2.5) and by the ohmic losses in
the FP plates, as discussed below.
An FP consists of two parallel partially reflecting plates between which multiple reflection occurs, creating constructive interference for the transmitted beam.
The construction of the Fabry-Pérot etalons is shown in Figure 2.9. The Moving Plate is suspended on Leaf-Springs between the Back Plate and the Fixed Plate. Each corner of the moving plate carries a loudspeaker-like Drive Coil which operates in a gap surrounding a permanent magnet in the Back Plate. The position of each corner, relative to the Fixed Plate, is determined by measuring the charge on the Capacitance Micrometer, formed by pads on the Moving and Fixed Plates. The position of each corner is controlled by a servo-mechanism which supplies sufficient current to the Drive Coil to make the measured charge equal to a control value. Initially, the two plates of the etalon are made parallel by applying offset signals to two of the three drive circuits. The moving etalon is then scanned as a whole by applying the same additional driving signal to all three coils.
The fixed and moving plates carry the reflecting elements, made of
free-standing nickel meshes supplied by Heidenhain: these meshes are affixed
to the Mesh-Mounting Frames which are attached to the plates. The meshes
consist of a rectangular grid of rectangular section: the thickness of the
meshes is 3![]() m, the width of the `bars' of which the meshes
are composed is 6
m, the width of the `bars' of which the meshes
are composed is 6![]() m, and the periods of the grid are 19
m, and the periods of the grid are 19![]() m
for the long wavelength Fabry-Pérot and 15.5
m
for the long wavelength Fabry-Pérot and 15.5![]() m for the
short wavelength Fabry-Pérot. The narrow tolerance allowed on these
dimensions is critical to the performance of the instrument.
m for the
short wavelength Fabry-Pérot. The narrow tolerance allowed on these
dimensions is critical to the performance of the instrument.
For monochromatic input, the transmitted intensity,
![]() ,
has a series of maxima dependent on the wavelength,
,
has a series of maxima dependent on the wavelength, ![]() , and plate
separation,
, and plate
separation, ![]() , as prescribed by the function (Born & Wolf 1970,
[1]):
, as prescribed by the function (Born & Wolf 1970,
[1]):
where ![]() is the phase difference between adjacent transmitted
rays and
is the phase difference between adjacent transmitted
rays and ![]() and
and ![]() are the single plate reflected and
transmitted intensities respectively. This can be simplified by defining the
parameter
are the single plate reflected and
transmitted intensities respectively. This can be simplified by defining the
parameter ![]() such that:
such that:
| (2.3) |
giving:
To take into account the intensity absorbed by the plates, ![]() ,
we apply:
,
we apply:
Now using Equation 2.5 in Equation 6.2 and rearranging we have:
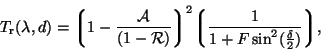 |
(2.6) |
where the first term on the right hand side expresses the wavelength dependent FP efficiency and the second factor is called the Airy Function.
The sharpness of the fringes is given by the Full Width Half Maximum (FWHM).
A useful parameter to use is the reflective finesse,
![]() , which is the ratio of the separation of successive orders
divided by the FWHM of the transmitted peaks.
Using this definition and writing the phase difference of the
, which is the ratio of the separation of successive orders
divided by the FWHM of the transmitted peaks.
Using this definition and writing the phase difference of the
![]()
![]() peak as
peak as
![]() where
where ![]() is the phase
shift from the line peak to its half power point, we see that:
is the phase
shift from the line peak to its half power point, we see that:
| (2.7) |
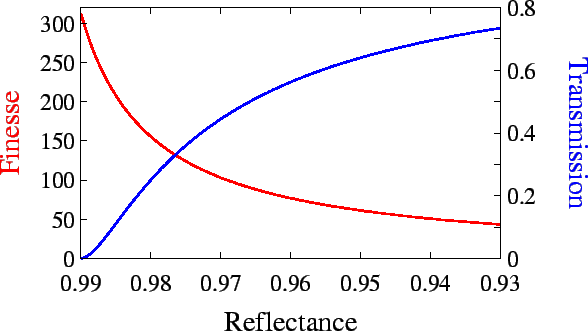
For a high resolving power, a finesse as large as
possible was required. However, measurements by Davis et al. 1995,
[12] indicate that the plate absorption
was ![]() 1%. As can be seen from
Figure 2.10, for a 1% absorption and 97%
reflectance (which corresponds to a finesse of 100), the transmission
is 44%. Increasing the reflectivity to 98% increases the
resolving power but decreases the transmission to
25%. For 99% reflectivity (and 1% absorption) the finesse is
very high, 312, however there is very little transmission.
1%. As can be seen from
Figure 2.10, for a 1% absorption and 97%
reflectance (which corresponds to a finesse of 100), the transmission
is 44%. Increasing the reflectivity to 98% increases the
resolving power but decreases the transmission to
25%. For 99% reflectivity (and 1% absorption) the finesse is
very high, 312, however there is very little transmission.
|
With metal mesh reflection plates, the reflectivity is wavelength
dependent (Davis et al. 1995, [12]).
Typically the reflectivity changes from about 0.96 to 0.98 for a
frequency change of a factor of two.
It is therefore impossible to cover the
whole LWS range with both high finesse and good transmission.
For this reason two FPs were used in the LWS: The Short wavelength
FP (FPS) to cover the wavelength range of 47-70![]() m and the
Long wavelength FP (FPL) for the range 70-196.6
m and the
Long wavelength FP (FPL) for the range 70-196.6![]() m.
m.
In wavenumber space, evenly separated peaks are produced by an FP. To
avoid spectral contamination it was required that when a particular order
is scanned across the grating response function of width ![]() ,
by varying the plate separation,
,
by varying the plate separation, ![]() , no other FP
orders would overlap with it (shown at the bottom of
Figure 2.5).
So for orders separated by
, no other FP
orders would overlap with it (shown at the bottom of
Figure 2.5).
So for orders separated by ![]() wavenumbers it is required that
the distance between the two meshes is:
wavenumbers it is required that
the distance between the two meshes is:
Since the grating resolving power is constant in wavelength terms, the
criterion for setting the FP gaps (![]() ) needs to be determined for the
shortest wavelength observed. The wavelengths of 45
) needs to be determined for the
shortest wavelength observed. The wavelengths of 45![]() m
(222cm
m
(222cm![]() ) and 90
) and 90![]() m (111cm
m (111cm![]() ) were used2.1 for FPS and FPL, respectively.
The spectral resolution of the grating in wavenumber units is
2cm
) were used2.1 for FPS and FPL, respectively.
The spectral resolution of the grating in wavenumber units is
2cm![]() and 1cm
and 1cm![]() respectively at the short wavelength extremes
of FPS and FPL. This results in a basic mesh separation
of 2.7mm for FPS and 5.0mm for FPL from
Equation 2.8. The actual motion required to
scan the whole LWS range using the ten detectors was reduced to a
small interval of
respectively at the short wavelength extremes
of FPS and FPL. This results in a basic mesh separation
of 2.7mm for FPS and 5.0mm for FPL from
Equation 2.8. The actual motion required to
scan the whole LWS range using the ten detectors was reduced to a
small interval of ![]()
![]() , the displacement required to move the
, the displacement required to move the
![]() peak to the
peak to the
![]() peak. For
the LWS this was at most
peak. For
the LWS this was at most ![]() 35
35![]() m for FPS and
m for FPS and ![]() 100
100![]() m
for FPL.
m
for FPL.
The order of radiation at wavelength ![]() is found from
is found from
![]() , so that:
, so that:
| (2.9) |
hence at their shortest operational wavelengths FPS was used in the
120![]() and FPL in 111
and FPL in 111![]() order. At their longest
wavelengths they worked in orders
77 and 50 for FPS and FPL respectively. This gave a range in
resolving power for the FP of
order. At their longest
wavelengths they worked in orders
77 and 50 for FPS and FPL respectively. This gave a range in
resolving power for the FP of ![]() 5000 to 12000.
5000 to 12000.
Other factors can limit the resolving power of an FP, such as the Jacquinot criterion (a limit induced by imperfect collimation), flatness criterion (limited by imperfect flatness of the plates) and even non-parallelism between the plates. All of these factors were made to be small, compared to the basic wire grid limitations discussed above.
The bottom panel of Figure 2.5 shows the expanded
range for one particular grating setting for SW4 with the FPS in the beam.
With the grating at
an angle of ![]() , radiation of a wavelength 73.5
, radiation of a wavelength 73.5![]() m falls
on SW4. The Fabry-Pérot
etalons could be scanned such that any spectral region within the
grating bandwidth can be selected without contamination from
higher or lower FP orders. A high resolution scan
therefore required that the grating was stepped across the range of SW4
and within each step the FP was scanned across the grating
spectral band. High resolution observations of
the first order wavelengths were made in the same way, but using FPL
with detectors LW1-5.
m falls
on SW4. The Fabry-Pérot
etalons could be scanned such that any spectral region within the
grating bandwidth can be selected without contamination from
higher or lower FP orders. A high resolution scan
therefore required that the grating was stepped across the range of SW4
and within each step the FP was scanned across the grating
spectral band. High resolution observations of
the first order wavelengths were made in the same way, but using FPL
with detectors LW1-5.
In this mode it was only possible in principle to use the output from
one detector at a time, since it would be unlikely that the FP
position and the grating position would be correct for any of the
other four detectors in the FPS range2.2.
It is therefore apparent that the LWS was very
efficient when recording medium spectral resolution with the grating,
but inefficient when observing the whole spectrum at high
resolution. Indeed, for line work using the Fabry-Pérots, most scans
were performed just around the known lines, which were evident from the
grating spectra.