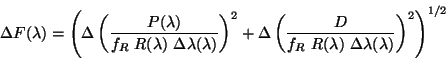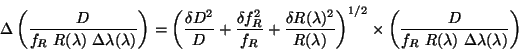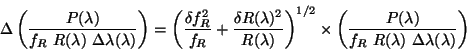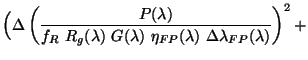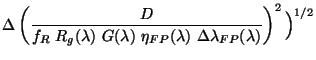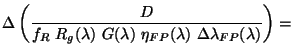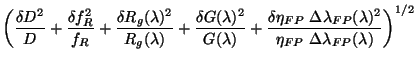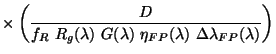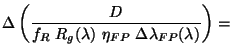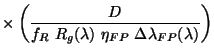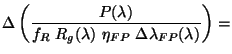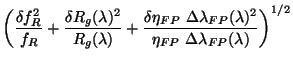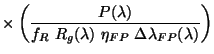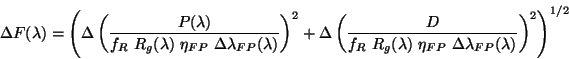



Next: 4.5 Processing of the
Up: 4. Data Processing
Previous: 4.3 Derive-SPD Processing Steps
Subsections
4.4 Auto-Analysis Processing Steps
4.4.1 Absolute responsivity correction and responsivity drift
correction
The LWS photoconducting detectors usually drift upwards in responsivity
with time owing to the
impact of ambient ionising radiation. This drift in responsivity must be
corrected for before co-adding of individual scans. This is referred to as
the responsivity drift correction.
The absolute flux calibration on the other hand, involves
referring the responsivity of the detectors at the time of the observation
to the responsivity at the time of the calibrator (Uranus) observation.
This is referred
to as the absolute responsivity correction.
Both corrections make use of the response to a standard illuminator flash
sequence performed before and after each observation. The following sections
describe
how these corrections are performed.
From Version 7 of the pipeline onwards the responsivity drift correction
was only performed for AOTs L01 and L03. This is because the correction did not
work very sucessfully for L02 and L04 AOTs. The keyword LORELDN in the
LSAN
header indicates if the responsivity drift correction has been performed or
not.
Before these corrections are applied, the data must be divided into `groups'.
Each group will
have a separate responsivity drift correction and absolute responsivity
correction calculated and
applied. The LGIF,
group information file, contains one record for each group.
The LGIF file identifies the start and end ITK of each group and also
records
information which is constant over the group. This includes the absolute
responsivity and responsivity drift correction information for the group.
The grouping of data depends upon the AOT type. The easiest way of describing
the grouping is to define the condition for the current group to end and a
new group to start. A new group starts when:
- An illuminator flash occurs.
- A new raster position starts.
This is checked for by looking for
changes in the raster point ID. However, in the case of solar tracking
observations the raster point ID is ignored as it can change even
when the raster position is the same.
- The observation is an L03 and the grating position changes.
A small amount of variation in the grating position is allowed
before it is regarded as `changed'. This is because only the
grating measured position is available and this is subject to
small fluctuations even when at the same nominal position.
For each group identified, a single reference time is calculated. This
is the point at which the absolute responsivity correction will be
calculated
for the group. It is also the point where the responsivity drift
correction will be normalised.
The reference time is simply half way between the time of the start and
end of the group. This reference time is written into the
LGIF file.
4.4.1.2 Absolute responsivity correction
Processing of illuminator flashes
The first stage of the absolute responsivity correction is to process each
illuminator flash in the observation. The aim is to find for each flash the
ratio between the detector photocurrents from the flash and the reference
photocurrents stored in the
LCIR calibration file.
Only the `closed' illuminator flashes are used for the absolute responsivity
correction. However, all illuminator flashes are first processed using the
same method. The results of processing each flash are written into the
LIAC
file. This file contains one record for each flash in the observation.
The data for all illuminator flashes in each observation are read
from the LIPD
data file produced by SPL. This file contains the detector
photocurrents for each ramp in each flash, plus the illuminator commanded
status word and other information.
Background determination
The first stage of processing an illuminator flash is to determine the
background photocurrent for each detector. These backgrounds will also be
used in the dark current/straylight subtraction stage (see
Section 4.4.2). The background value for each
detector for each flash is written into the
LIAC file.
The method for determining the background is as follows:
- Extract the set of detector photo currents in the LIPD file
corresponding to the background measurement taken at the
start of the flash.
- Perform median clipping on the set of photo currents for each detector
This is to remove spurious values due to undetected glitches. See
below for a description of median clipping. The
keyword LCIRNSDB in the
LCIR
file header gives the number of standard
deviations to use for median clipping of the background.
- Average the set of photo currents for each detector to determine
a single background value for each detector.
The uncertainty to be associated with
this value is given by
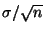 for the set of averaged
photo currents. If there are less than three photo current
values then the maximum of the individual photo current uncertainties
is used.
for the set of averaged
photo currents. If there are less than three photo current
values then the maximum of the individual photo current uncertainties
is used.
Median clipping
The purpose of median clipping is to remove any outlying values from a set of
measurements of the same value.
There must be at least five values for median clipping to be performed.
The method for median clipping is as follows:
- Calculate the median value of the set of points.
- Calculate the standard deviation of the set of points, omitting the
highest and lowest values in the set.
- Check each point and reject any that are more than a predetermined
number of standard
deviations above or below the median value. The number of standard
deviations depends
upon the data which is being median clipped.
Ratioing against reference data
For each illuminator flash a single absolute responsivity ratio is calculated
for each detector. This is done by ratioing the photocurrents in the
illuminator flash against reference flash data in the
LCIR
calibration file.
The final ratio for each detector is written into the
LIAC file.
The method for calculating the ratio for each detector depends on the kind
of illuminator sequences performed in the observation. There was a major
change
in the on-board illuminator operations after ISO revolution 442. For all
observations performed after revolution 442, the number of integrations
performed for each
illuminator were increased from 8 to 24.
Before revolution 442
Prior to ISO revolution 442 the removal of points affected
by glitches sometimes left just three or four points for an
individual illuminator, making it almost impossible to apply the OLP
Vesion 10
weighted-average method (see below).
Therefore, even in OLP Version 10,
these data are still processed using the 'OLP 8'
illuminator processing method.
This method
relies on using the point-by-point ratio of detector photocurrents
from the measured and references flashes.
The following sequence of
steps is performed:
- Determine the `type' of the illuminator flash for the current
observation. The illuminator flash type is determined from the
revolution number of the observation. The LCIR file header should
describe each of the possible flash types and the range of
revolution numbers in which they occur.
- Locate the start of the data for the appropriate flash type in
the LCIR file.
- Locate the start of the illuminator flash data in the
LIPD file. The
data from the background measurement at the start of the flash are
skipped.
- For each photo current value for each detector in the LIPD
file, subtract the appropriate background (see
Section 4.4.1),
then divide by the corresponding entry in the LCIR file. Continue
until no more entries remain in the LCIR file.
Skip any photocurrent values which are set to zero in the LIPD file
or the LCIR file. Skip any values for which the status word in the
LCIR file indicates that it should be ignored.
If, while doing this, data are found to be missing from the LIPD file
then jump to the start of the next illuminator level in the LIPD
and LCIR files. Missing data are detected by a mismatch between
the illuminator commanded status value in the LIPD and LCIR
records. The warning message `LIMM' is issued each time this
occurs. Data may be missing from the LIPD file because of
telemetry dropouts or frame checksum errors. The LCIR file should not
have any missing data.
- Perform median clipping on the set of ratios calculated for each
detector. This is to discard outliers due to undetected glitches etc. See Section 4.4.1.2 for a details of median clipping.
The value of the keyword LCIRNSDF in the LCIR file header
gives the number of standard deviations for median clipping.
- Find the average of the remaining ratios for each detector. The
result is a single responsivity correction factor for each
detector. The uncertainty for each value is calculated using
the standard error formula (
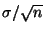 ).
).
After revolution 442 (the `OLP 10' method)
For observations performed after revolution 442, with the new illuminator
scheme, the `OLP 10' method is used. It calculates the detector
response correction factor using weighted-averages of the photocurrent
ratios. The key processing steps are as follows:
- Calculate the point-by-point ratio of the photocurrent in the observed
flash sequence and the reference flash sequence.
- Group these ratios according to the illuminator in operation. Five
such groups will occur because there are five illuminators.
- Calculate the variance of each group of ratios.
- Calculate the weighted-average of these ratios, using the variances
of the groups as weights.
- Repeat steps 1 to 4 for all other flashes in the observation.
- Calculate the average of the correction factors from all flashes
in the observation.
These steps can be expressed in the following equations:
![\begin{displaymath}
R(d,j)=\frac{\sum_{i=1}^{5} \left[ \frac{r(d,i,j)}
{\sigma...
...
{\sum_{i=1}^{5} \left[ \frac{1}{\sigma_r(d,i,j)} \right]^2}
\end{displaymath}](img163.gif) |
(4.7) |
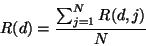 |
(4.8) |
where 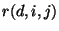 and
and
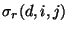 are the response correction factor
and standard deviation respectively for detector
are the response correction factor
and standard deviation respectively for detector 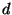 ,
illuminator
,
illuminator 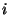 and flash
and flash 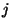 ;
; 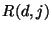 represents the weighted average of the response correction factor for detector
represents the weighted average of the response correction factor for detector
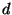 and flash
and flash 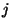 ; and
; and
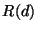 is the final response correction factor for detector
is the final response correction factor for detector 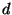 after
averaging over the
after
averaging over the 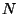 flashes in the observation.
flashes in the observation.
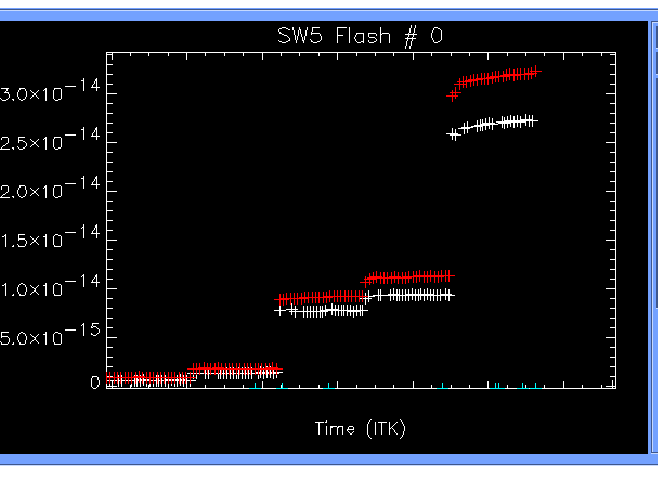
This method is expected to be an improvement on the `OLP 8' method because
the response of the LWS detectors is known to be transient
(Fouks 2001, [16] and Caux 2001, [5]),
leading to a
characteristic signature of the detector photocurrent for each illuminator
as shown in Figure 4.4. In other words the
scatter of photocurrent ratios for a given illuminator is not
just pure statistical noise but is instead a systematic feature of the given
detector.
Figure 4.4:
Illuminator flash sequence
photocurrents for detector SW5 in one observation
carried out after ISO revolution 442 (white plus symbols).
The reference illuminator flash data for this detector are
shown as red plus symbols. The x-axis is a measure
of the LWS on-board instrument time, ITK (Instrument Time Key).
|
|
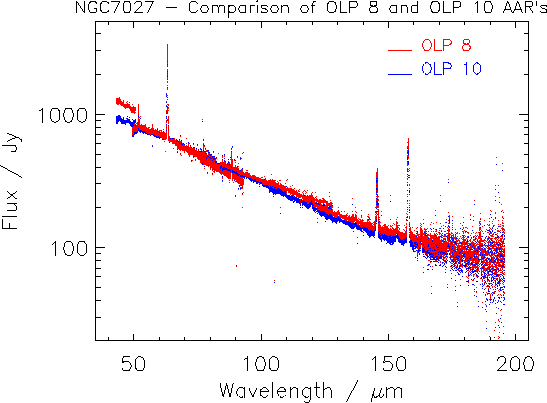
Figure 4.5 shows the spectrum of NGC 7027
respectively after application of both the `OLP 8' and `OLP 10' methods of
illuminator processing. The level
of continuity across the detectors in the `OLP 10' method can be clearly seen.
Numerous other test cases and examples have confirmed the superiority of this
method. We therefore conclude that the new illuminator processing method as
implemented in OLP Version 10 is superior
to the one in OLP Version 8 and leads to better stitched spectra. For off-axis point
sources in the
LWS beam or for extended sources, any residual discrepancy present between
adjacent
detectors, especially in the SW detectors, is most likely to be the result
of the asymmetric LWS
beam profile (Lloyd 2001, [28]).
Figure 4.5:
Comparison of `OLP 8' and `OLP 10' methods of illuminator
processing for NGC 7027.
|
|
Performing correction
Once all illuminator flashes have been processed the absolute responsivity
can be derived.
For each group identified in the LGIF file the absolute responsivity ratio
for each detector at the reference time is calculated. This is done
using the data from the two closed illuminator flashes which surround the
reference time. For each detector the absolute responsivity correction
factor is calculated by doing a linear interpolation in time between the
values at the two surrounding closed illuminator flashes. The uncertainty
in this value is calculated as the highest of the uncertainties for the
two surrounding values. The value of the
correction factor and its uncertainty are written into the LGIF file.
The absolute responsivity correction is then performed on all of the
science data within the group by subtracting the dark current from the
detector photocurrent and then simply dividing the result by the absolute
responsivity correction factor.
4.4.1.3 Responsivity drift correction
The responsivity drift correction corrects for the `drift' in responsivity
during an observation. The drift is obtained from the information in the
LSCA
scan summary file. The responsivity drift is calculated separately for
each group of data identified in the LGIF file.
The responsivity drift correction is only performed for AOTs L01 and L03. No
drift correction is performed for AOTs L02 and L04.
Generation of LSCA, scan summary file
The LSCA scan summary file contains summary information for every scan
in the
observation. This includes a value which represents the signal level over
the
whole scan. This is calculated by finding the average signal per point in
the
scan. The signal values used are the values from the LSPD file, before any
further processing. Any values which are marked as `invalid' in the LSAN
status word are not included in this average.
For each scan a reference time is also calculated. This is simply the mid
point between the times of the start and end of the scan.
Note that for L02 photometric observations no LSCA file is produced. This is
because no responsivity drift correction is needed on this data. Also, since
AAL regards each point in a photometric observation as a single scan, the LSCA
file would be very large and would contain the same information as the LSAN
file.
Determination of drift slope
For each group of data identified in the LGIF file a separate drift
slope is calculated for each detector. The method is as follows:
- Identify the data in the LSCA scan summary file which lie within the
time range of the group.
- Discard any data from the LSCA file which does not correspond
to a `full' scan. The last scan in a measurement is often a `short'
scan where the mechanism only covers a fraction of the previous
`full' scans.
Short scans are identified by comparing the total number of
points (ramps) in each scan with the number of points in the first
scan in the group. The first scan of a group is assumed to be a
full scan. If the number of points in a scan is below half of the
number in a full scan then it is classified as a short scan and
discarded.
Note that the total number of ramps in a scan can also vary because of
missing frames of telemetry data.
- For each of the full scans identified in the LSCA file, for each
detector, fit a first order
polynomial to the set of average signal values against reference
times. This is done using a least squares fitting algorithm. The
coefficients of the fitted slope are written into the LGIF file.
The coefficients give the LSPD value at the reference time for the
group and the gradient of the slope in LSPD units per time unit.
Note that in certain cases there may be insufficient valid data to determine
a drift slope. This can happen for the inactive detectors in FP observations.
The flag LGIFRSTA in the LGIF file indicates when this happens.
In this case no responsivity drift correction is performed.
Performing correction
Once the drift slopes have been calculated for each detector in each group
the responsivity drift correction can be applied.
For each group identified in the LGIF file the corresponding flux
data are corrected. The method for correction is as follows:
- Find the Y value of the drift slope for the appropriate detector at
the time of the point to be corrected.
- Divide this by the Y value of the drift slope at the reference
time for the group. This gives the relative drift normalised
to the reference time of the group.
- Divide the flux value by the ratio determined above. The
uncertainty in flux value is not changed.
4.4.2 Dark current/background straylight subtraction
Each observation contains at least two `closed' illuminator flashes. During
these illuminator flashes the wheel is set to an opaque position, removing
the flux contributions due to the source. This is achieved by placing
one of the FPs in the beam with the etalons misaligned. For grating
observations, at least the first and last flashes in the observation will be
closed flashes. For FP observations, all flashes are closed flashes since the
FP is already in the beam and the etalons are misaligned before the
illuminator flash is taken.
The background measurements during these closed illuminator flashes are a
measure of the `dark signal' at the time they were taken. (The `dark
signal' is the sum of the dark current and straylight). There is a
separate background value for each detector. The values for the background
measurements for the closed illuminator flashes are calculated using the
information in the LIPD file. See Section 4.4.1 for details
of how the background values are calculated.
The backgrounds for each illuminator flash in the observation are written
into the LIAC file. The closed illuminator flashes in the LIAC file are
identified by the wheel absolute position field being set to either 0 (FPS)
or 2 (FPL).
Between each pair of closed illuminator flashes in the observation a single
dark current/straylight value is calculated for each detector. This is
done by taking the mean of the two values from the surrounding flashes.
The uncertainty in this value is given by the maximum of the two
uncertainties from the surrounding flashes.
The dark current/straylight value is then subtracted from all of the
detector photocurrent values between the pair of illuminator flashes.
The uncertainty in the photocurrent is calculated by adding the
uncertainties in the dark current/straylight and input photocurrent in
quadrature. The dark current/straylight value subtracted from each
scan is written into the scan summary file (LSCA).
See Section 7.2.7.4 for details of the LSCA file.
From Version 8 onwards OLP uses a fixed dark current for processing of
Fabry-Pérot data (AOTs L03 and L04).
In OLP Version 10, for grating observations AAL checks each scan of each
detector to see if the fixed dark current produces a better result
(i.e. flux less negative) than the
measured dark current. If this is the case then the fixed dark current
is used instead of the measured dark current.
The values for this fixed dark current (one value
per detector) have been
determined as explained in Section 5.4 and are stored in the
LCDK calibration file.
4.4.3 Grating scan wavelength calibration
The grating mechanism positions are converted into wavelengths at this
stage. The input to this stage is the grating measured positions
(LVDT readouts) and
the calibration information in the LCGW file (see
Section 7.3.2 for a description of the LCGW file).
The conversion is performed by means of an algorithm. The
coefficients required for the algorithm are stored in the LCGW file.
It has been found that the relationship between LVDT and wavelength changed
over time. The LCGW file therefore contains different coefficients for
different time periods.
The wavelength conversion is performed in two steps. The first step is to
calculate the input beam angle to the grating, 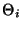 , for all ten
detectors. This is calculated using the following formula:
, for all ten
detectors. This is calculated using the following formula:
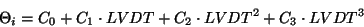 |
(4.9) |
Where:
- LVDT is the grating measured position.
-
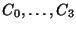 are the time varying coefficients of the fit.
These are obtained from the LCGW file.
are the time varying coefficients of the fit.
These are obtained from the LCGW file.
The input beam angle is then converted into wavelength for each detector by
applying the grating equation and the geometry applicable to that detector.
This is done using the following formula:
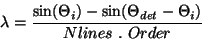 |
(4.10) |
Where:
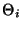 is the input beam angle.
is the input beam angle.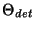 is the detector angle, obtained from the LCGW file.
is the detector angle, obtained from the LCGW file.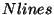 is the number of lines per
is the number of lines per 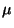 m on the grating. This is a
fixed value, obtained from the LCGW file.
m on the grating. This is a
fixed value, obtained from the LCGW file.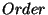 is the fixed order number for the detector. This is 1
for the LW detectors and 2 for the SW detectors.
is the fixed order number for the detector. This is 1
for the LW detectors and 2 for the SW detectors.
4.4.4 Grating spectral responsivity calibration
The efficiency of the LWS as a spectrometer varies with wavelength,
mainly due to the bandpass filtering incorporated into each detector unit
and the spectral response of the detector itself.
The Grating Relative Responsivity Wavelength Calibration file,
LCGR (see Section 7.3.2), contains a
spectrum of the relative response of the instrument in grating mode
(The way the file is derived is described in
Section 5.2). The
wavelength for each point in the spectrum is looked up in this table
and the corresponding responsivity value read. If no exact wavelength
match is found within the table then a responsivity value is calculated
by linear extrapolation between surrounding wavelength entries.
The responsivity
corrected flux then is calculated by dividing the flux by the
responsivity value.
From OLP Version 7 the wavelength range in the LCGR file was
extended compared to the previous versions. This is to allow for wavelength
identification of features on overlapping detectors
(See Figure 2.5). The relative photometric
calibration at the edges of the range is very poor.
Many detectors have a `steep sided' spectral response which makes the
removal of the response uncertain. Also the steep sides enhance the effect
of transient responses and the low throughput at the edges of the response
curves leads to low signal-to-noise ratios.
This region should therefore not be
used for anything except wavelength identification of features. Data in this
region can be identified by means of the `grating spectral responsivity
warning' flag in the LSAN status word (see Section 7.2.8).
When this warning flag is set this indicates that the data point has poor
calibration and should not be used for anything other than wavelength
identification. The wavelength ranges for which the LCGR calibration is
nominal are also specified by keywords
in the LCGR header (see Section 7.3.2.)
4.4.5 Spectral bandwidth correction
This correction only concerns grating scans. (For the corresponding
correction for the FPs, see Section 4.4.7.)
The LCGB calibration file contains the spectral element size
and uncertainty for each of the ten detectors. Auto-Analysis simply
divides the flux for each
detector by the appropriate spectral element size to perform the correction.
The new flux uncertainty is calculated using the standard error formula.
The values of the spectral element sizes and uncertainties are written as
keywords into the header of the LSAN file. Keywords LCGBddd contain
the spectral element size for detector ddd (ddd='SW1'...'LW5'), while
keywords LCGBUddd contain the corresponding uncertainties.
4.4.6 Fabry-Pérot scan wavelength calibration
The wavelength calibration of a FP scan is done using a parametrised
algorithm for the FP wavelength calibration.
The wavelength calibration for FP spectra is done as follows:
- The grating position (LVDT value) is converted to wavelength using
the algorithm specified above for the grating scan wavelength
calibration (Section 4.4.3).
- For every point in the scan the position value of the FP is
converted into a gap of the two Fabry-Pérot etalons. This is done
using the third order polynomial:
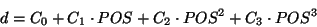 |
(4.11) |
where 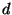 is the gap of the FP etalons,
is the gap of the FP etalons, 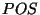 is the FP position
value (as stored in the SPD product file (see
Section 7.2.5), and
is the FP position
value (as stored in the SPD product file (see
Section 7.2.5), and 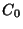 ,
, 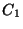 ,
, 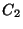 and
and
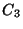 are the FP wavelength calibration parameters read from
calibration file LCFW (see Section 7.3.2).
are the FP wavelength calibration parameters read from
calibration file LCFW (see Section 7.3.2).
- The first point of the scan is then used to determine the order the FP
was working at for this scan. For this the wavelength determined from
the grating position is taken as the approximate wavelength of
the first point of the spectrum. The order is then calculated from:
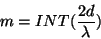 |
(4.12) |
where 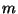 is the order of the scan,
is the order of the scan, 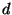 is the gap of the FP
etalons and
is the gap of the FP
etalons and 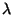 is the wavelength. INT means the integer
part of this division.
is the wavelength. INT means the integer
part of this division.
- Using the order calculated in the previous step, all Fabry-Pérot
gaps for the points in the spectrum are converted to wavelength using:
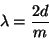 |
(4.13) |
4.4.7 Fabry-Pérot throughput correction
From OLP Version 8 onwards, the FP spectral responsivity calibration
has been replaced by the FP `throughput' correction, which is the
product of the FP
transmission multiplied by the FP resolution element. The method of
calibrating the total throughput of the FP's has been devised using Mars as
a calibration standard. This method uses a fitted polynomial between
the wavelength and the FP throughput and the results are FP fluxes
in units of W cm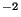
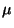 m
m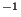 .
.
The grating spectral responsivity calibration, described in
Section 4.4.4, is also applied to FP data.
4.4.8 Velocity correction to wavelength
The wavelengths calculated in the previous stages are corrected for the
velocity of the spacecraft and earth towards the target. The header of
the LSPD file contains keywords which specify this velocity at three
points during the observation. These keywords are written by a subroutine
written by ESA which is external to the LWS pipeline (TREFDOP1 to 3).
The velocity at each mechanism position in a scan is calculated by
interpolating in time between the three given values. A second order
curve fit is used for the interpolation. Once calculated, the
coefficients of this fit are written into the LSAN header as the
keywords LVCOEFFn (n=0-2).
The wavelength at each mechanism position is then corrected using the
following formula:
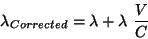 |
(4.14) |
Where:
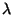 is the wavelength to be corrected, in
is the wavelength to be corrected, in 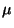 m.
m.- V is the velocity of the spacecraft and earth towards the target,
in km/s.
- C is the speed of light in km/s.
4.4.9 Write LSNR data product (only in OLP versions earlier than 8)
Up to OLP Version 7, the absolute responsivity and the responsivity drift
corrections were determined at the end of AAL. Therefore
at this stage, before these corrections, the results of the previous
calibration steps were written into the
first product file produced
by Auto-Analysis, named LSNR. This file was
identical in structure to the final LSAN file, apart from a few minor
differences. This file was provided to give
observers access to the data before the absolute responsivity correction and
responsivity drift corrections were applied. In a few cases these corrections
did not work sucessfully. The LSNR file provided an alternative product file
for those cases. After OLP Version 8 the responsivity corrections
are performed at the start of the pipeline.
4.4.10 Calculation of uncertainties
The LSAN file contains the field LSANFLXU which gives the estimation of the
systematic flux error. The calculation of the uncertainty is detailed
below,
for the grating (AOTs L01 and L02) and the Fabry-Pérot (AOTs L03 and L04).
4.4.10.1 Grating continuum flux error estimation
The grating flux is given by:
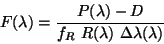 |
(4.15) |
where 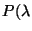 ) is the photocurrent; D the dark current;
) is the photocurrent; D the dark current; 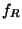 the
responsivity correction
factor from illuminator operation;
the
responsivity correction
factor from illuminator operation; 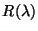 the detector responsivity
from the LCGR file
(
the detector responsivity
from the LCGR file
(
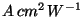 ) and
) and
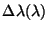 the equivalent width
of the grating resolution element at this
wavelength.
the equivalent width
of the grating resolution element at this
wavelength.
We can write the associated uncertainty as:
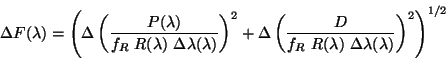 |
(4.16) |
where
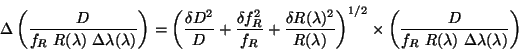 |
(4.17) |
and
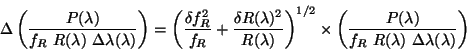 |
(4.18) |
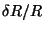 is the statistical error in the LCGR file. Since this error does
not depend on the observation, from OLP Version 10 it is left out of the
error calculation. This term is thus set to zero. The user is referred to
Section 5.2 for an estimate of the uncertainty of the
relative response function (LCGR file).
The value of
is the statistical error in the LCGR file. Since this error does
not depend on the observation, from OLP Version 10 it is left out of the
error calculation. This term is thus set to zero. The user is referred to
Section 5.2 for an estimate of the uncertainty of the
relative response function (LCGR file).
The value of
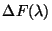 is thereby
calculated absolutely using equation 4.16 and placed in the
LSAN.LSANFLXU tag.
is thereby
calculated absolutely using equation 4.16 and placed in the
LSAN.LSANFLXU tag.
4.4.10.2 Fabry-Pérot continuum flux error estimation
For the Fabry-Pérot the flux is given by:
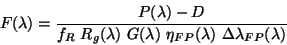 |
(4.19) |
where, in addition to the definitions above, 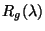 is the
detector responsivity in grating
mode at this grating setting (the RSRF value in
is the
detector responsivity in grating
mode at this grating setting (the RSRF value in
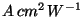 );
);
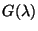 the relative height of
the grating resolution element profile at this wavelength;
the relative height of
the grating resolution element profile at this wavelength;
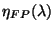 the Fabry-Pérot
efficiency at this wavelength and
the Fabry-Pérot
efficiency at this wavelength and
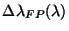 the
equivalent width of the Fabry-Pérot
resolution element at this wavelength (in
the
equivalent width of the Fabry-Pérot
resolution element at this wavelength (in 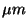 ).
).
We can write the associated uncertainty as:
where
Notice here that the error is quoted for the product
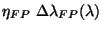 .
This is because the new
method of calibration for the FP throughput cannot distinguish between the
contribution from the transmission of the FP and that of the resolution
element of the FP.
Also from Version 8 of the OLP onwards, the grating resolution element
correction was not done; therefore, G(
.
This is because the new
method of calibration for the FP throughput cannot distinguish between the
contribution from the transmission of the FP and that of the resolution
element of the FP.
Also from Version 8 of the OLP onwards, the grating resolution element
correction was not done; therefore, G(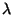 ) drops out.
The equivalent equations for the error arising from the photocurrent and dark
current are therefore:
) drops out.
The equivalent equations for the error arising from the photocurrent and dark
current are therefore:
and
All the terms except
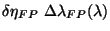 are known; this is calculated from a fit
to the error values in the original derivation of the
are known; this is calculated from a fit
to the error values in the original derivation of the
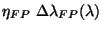 parameters.
The absolute flux error placed in the LSAN.LSANFLXU tag is therefore:
parameters.
The absolute flux error placed in the LSAN.LSANFLXU tag is therefore:
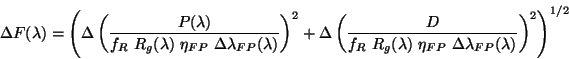 |
(4.24) |
Note that in this case also 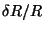 is set to zero in OLP Version 10
(see last paragraph of Section 4.4.10.1).
is set to zero in OLP Version 10
(see last paragraph of Section 4.4.10.1).




Next: 4.5 Processing of the
Up: 4. Data Processing
Previous: 4.3 Derive-SPD Processing Steps
ISO Handbook Volume III (LWS), Version 2.1, SAI/1999-057/Dc
![]() for the set of averaged
photo currents. If there are less than three photo current
values then the maximum of the individual photo current uncertainties
is used.
for the set of averaged
photo currents. If there are less than three photo current
values then the maximum of the individual photo current uncertainties
is used.
![\begin{displaymath}
R(d,j)=\frac{\sum_{i=1}^{5} \left[ \frac{r(d,i,j)}
{\sigma...
...
{\sum_{i=1}^{5} \left[ \frac{1}{\sigma_r(d,i,j)} \right]^2}
\end{displaymath}](img163.gif)