Subsections

• 5.12.1 Introduction
• 5.12.2 Strategy of calibration
  • 5.12.2.1 The line fitting algorithms
• 5.12.3 Calibration for OLP Version 10
• 5.12.4 Monitoring the Fabry-Pérot wavelength calibration
  • 5.12.4.1 Results for FPS
  • 5.12.4.2 Results for FPL
• 5.12.5 Fabry-Pérot wavelength accuracy

5.12 Fabry-Pérot Wavelength Calibration

5.12.1 Introduction

The LWS Fabry-Pérot interferometers are fully described in Davis et al. 1995, [12] but for this section, which explains the adopted strategy and the results of the wavelength calibration, we can simply think of a Fabry-Pérot as two partially transmitting mirrors facing each other, a distance apart.

Under simplifying assumptions the FP transmission has a maximum at wavelength when:

(5.8)

where is a positive integer called the 'order'. Note that at separation there are an infinity of transmitted wavelengths, namely , , and so on. To avoid contamination by undesired wavelengths the LWS FP used the grating as an order sorter.

In Equation 5.8 there are no free parameters so that once and are known we can easily derive without needing a calibration. But the separation between mirrors was read out by the on-board electronics in terms of a quantity, the FP encoded position, whose relation with is known from ground calibration to be a cubic function. So Equation 5.8 turns into:

(5.9)

Being the result of a digital measurement, is an integer running from 0 to 4095. Wavelength calibration means then deriving the four coefficients of the above polynomial.

5.12.2 Strategy of calibration

Let us assume that we have observed a number of lines at wavelengths and found their centres^5.1 . We can not directly invert Equation 5.9 to find the unknown coefficients because we still miss the orders . So that the first step is to observe the same line in at least two adjacent orders, say and .

The AOT logic selected for each wavelength one single order, so to observe the same line at different orders we executed special dedicated observations (COIF). Having determined the centres and for the two orders we recast Equation 5.9 in a different form:

(5.10)

After observing lines in different orders a first estimate of the coefficients is obtained with a least squares fit. Now we rewrite Equation 5.9 in the following way:

(5.11)

where refers to a given wavelength observed at order . All the 's must be integer so that the value of which minimises the differences is looked for. Once is found Equation 5.9 is used to determine the order and finally all four coefficients can be derived at the same time, again using a least squares fit.

5.12.2.1 The line fitting algorithms

To find the centre of a line three algorithms can be used and are now briefly described.

The three techniques are completely independent of each other and give us a better estimate of the centre position and its error, defined as with being the average of the three values .

However, the FP wavelength calibration was carried out according to the procedure described in the previous section and uses only the first method described below. All three techniques have been used for the monitoring programme discussed later.

• Determination of the centroid
  The background is estimated, and then subtracted, by fitting a low order () polynomial to the ends of the FP scan, far from the line. The line profile is divided into a number of points, usually 10, avoiding the wings and the peak where the profile could be distorted, e.g. by memory effects.

  At each point the segment that intersects the line is found and the half-power point computed. The 10 half-power points are then averaged. The procedure, fully described in the LWS Calibration File Derivation Procedure, gives as output:

  • the peak position and its error;
  • the peak flux in term of photocurrent;
  • the full width at half maximum (FWHM).
• Fourier interpolation
  The background is estimated as in the previous method. The line is then Fourier transformed and all the high frequencies filtered out. After an inverse transformation the obtained smoothed line profile is reconstructed to find the peak position and intensity as well as the FWHM.
• Gaussian fitting
  The IDL procedure GAUSSFIT has been used. It simultaneously fits the background and the line profile so from this point of view it is the best of the three methods presented. The procedure gives the line centre, peak height and FWHM. In all cases the FP line profile is definitively not Gaussian, being the convolution of the source intrinsic profile and an Airy function so that only the centre position is reliable.

Experience has shown that even at low signal-to-noise ratio, the three line centres very rarely differ by more than one FP encoded position.

5.12.3 Calibration for OLP Version 10

Lines and sources observed to calibrate the short wavelength FP (FPS, covering from m to m) and for the long wavelength FP (FPL, covering from m to m) are reported in Table 5.17. The derived coefficients are written in Table 5.18.

Table 5.17: Lines and sources used to calibrate the FP's. Rev. is the revolution number.

	Source	Rev.	Ion	Line	Orders
				[m]
FPS	NGC 7027	168	[O I]	63.2	87, 88
	G 36.3+0.7	300	[O III]	51.8	104, 105, 106
	G 0.60.6	321	[O III]	51.8	105, 106
	NGC 7027	370	[O I]	63.2	88, 89
FPL	NGC 7027	175	[O I]	145.5	69, 70
	G 0.60.6	287	[O III]	88.4	114, 115
	G 36.3+0.7	300	[O III]	88.4	114, 115

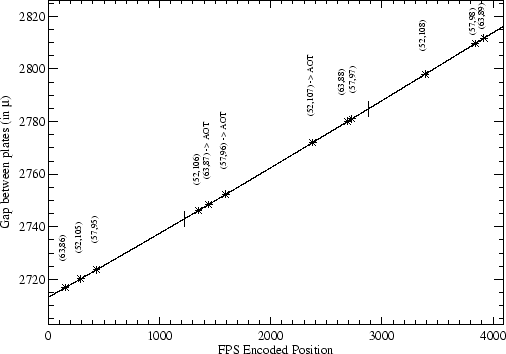
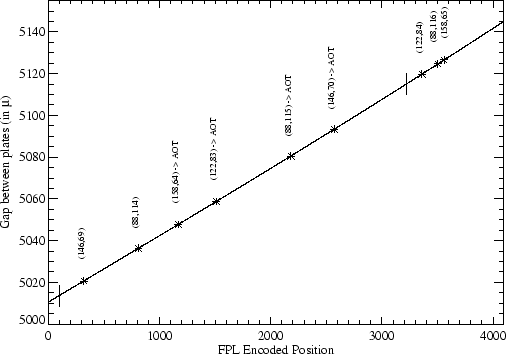
In Figure 5.25 the relation between encoded position and gap between plates is shown as a solid line for both FPS and FPL. Asterisks mark the positions where a particular combination falls. The combinations actually selected by the AOT logic are indicated. All wavelengths observable with FPS correspond to a particular position inside the portion of the curve delimited by two vertical segments.

Figure 5.25: Distance between plates versus encoded position for FPS (top) and FPL (bottom) wavelength calibration coefficients. The instrument was always operated in the range delimited by the two small vertical segments. Note the larger interval of positions used for FPL. The asterisks mark the position corresponding to a particular combination (wavelength, order). To calibrate the instrument some other combinations were used, also shown in the figure.

Table 5.18: FPS and FPL wavelength calibration coefficients (see Equation 5.9).

	FPS	FPL
A	2713.2569	5010.6224
B	0.023870650	0.031654363
C	4.1581366  10	7.3574580  10
D	2.4636391  10	5.1097999  10

5.12.4 Monitoring the Fabry-Pérot wavelength calibration

To check the stability of the calibration against possible temporal trends, weekly observations have been performed on a number of selected sources, chosen according to their luminosity, visibility and with as small FWHM as possible. Lines and sources used for this task are listed in Table 5.19.

Table 5.19: Lines and sources used to monitor the FP calibration.

Ion	Line	FP	Source
	[m]
[O III]	51.8	S	G 0.60.6, G 36.30.7, NGC 7027, NGC 7538
[N III]	57.3	S	NGC 3603, G 0.60.6, NGC 6302
[O I]	63.2	S	NGC 7023, NGC 7027, NGC 7538, S106
[O III]	88.4	L	G 0.60.6, G 36.30.7, NGC 3603, NGC 7538
[N II]	121.9	L	G 0.60.6
[O I]	145.5	L	NGC 7023, NGC 7027
[C II]	157.7	L	G 0.60.6, NGC 6302, NGC 7023, NGC 7027,
			NGC 7538, S106

Each line has been fitted with the methods previously described so that its centre is the average of three values. It has been converted into wavelength using Equation 5.9 and taking into account the relative motion of the source with respect to the satellite.

5.12.4.1 Results for FPS

The calibration looks stable with no temporal trend. Note that the [N III] line was not used to derive the calibration coefficients, so that we can use our data to measure its rest wavelength. Combining all 11 measurements we get m, in perfect agreement with the quoted value in the literature (m). In Table 5.20 the rms error for each wavelength is reported.

Table 5.20: The rms calibration errors for each line observed as part of our monitoring programme for FPS.

Ion	Line	Error
		[m]	[km s]
[O III]	51.8	9.5	5.5
[N III]	57.3	7.2	3.8
[O I]	63.2	8.7	4.1

5.12.4.2 Results for FPL

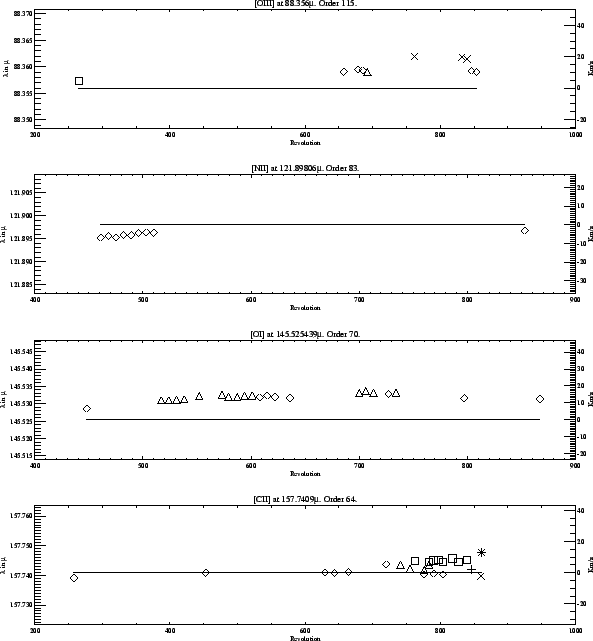
Figure 5.26 illustrates the monitoring of the FPL wavelength accuracy. As can be seen, especially in the plot corresponding to the [O I] line at 145.5 m, the calibration seems to be affected by systematic errors. But even in the worst case errors are lower than half a spectral resolution element.

Figure 5.26: Monitoring data for FPL. Solid line: rest wavelength. Left ordinate: wavelength in microns; right ordinate: difference from rest position in km s. Symbols: G0.6-0.6 (first 2 plots), NGC7023 (second 2 plots); G36.3-0.7 (first), NGC7027 (third and fourth); NGC3603 (top), NGC7538 (last); NGC7538 (first), S106 (last); for the last plot G0.6-0.6 and NGC6302.

The rms errors are reported in Table 5.21. Note that when the measured wavelength is systematically shifted with respect to the rest wavelength, the rms is a measure of the average displacement and not a true scatter around the mean.

Table 5.21: The rms calibration errors for each line observed as part of our monitoring programme for FPL.

Ion	Line	Error
		[m]	[km s]
[O III]	88.4	1.5	5.1
[N II]	121.9	2.2	5.4
[O I]	145.5	6.6	13.6
[C II]	157.7	3.0	5.6

5.12.5 Fabry-Pérot wavelength accuracy

As is clear from Equation 5.8 or 5.9 in Section 5.12, what we measure is the distance and not the wavelength . For this reason the accuracy of the calibration depends on which FP position range was used to observe a given line. This information is written in LSPD files.

Looking at Figure 5.25 (top) and Table 5.20 we conclude that the accuracy of the wavelength calibration for FPS is 4km s at positions , slightly increasing to 6 km s at larger values of . A reasonable choice for error over the range of positions is then .

In the case of FPL the range covered by the instrument is larger. From Figure 5.25 (bottom) and Table 5.21 it is evident that a systematic error is present in the calibration, increasing towards larger values.

For the validation of OLP Version 10 data, the accuracy of lines was studied in NGC 7027 for 21 observations. Excluding the 145.5 m [O I] line, the overall rms error was 2.69 km s. Measurements of the 145.5 m line were made during orbits 601, 706, 713 and 734. If the rest wavelength is taken to be 145.525 m then the velocity residuals of these measurements are +16.1, +20.7, +18.2 and +18.2 km s, which makes the overall rms error 4.42 km s. However, if a value of 145.535 m is used, the velocity residuals are 4.50, +0.11, 2.37 and 2.37 km s, and the overall rms error is only 2.65 km s.

This discrepancy in the measurement of the 145.5 m line of NGC 7027 suggests that either:

this line arises from a region which has a different velocity signature compared to the other lines measured in NGC 7027. This is plausible given the complex nature of NGC 7027 (see Phillips et al. 1991, [32]). However, the [O I] line at 63.2 m observed with FPS did not show such high residuals in FPS, which makes this hypothesis difficult to believe.

the 145.525 m rest wavelength, the value used when deriving the wavelength calibration, is inaccurate.

A literature search has shown there are two different values recorded as the rest wavelength for the 145.5 m [O I] line:

145.525 m, from the NASA's Jet Propulsion Laboratory Spectral Catalog
-- see http://spec.jpl.nasa.gov/ and Zink et al. 1991, [47]

145.535 m, from The National Institute of Standards and Technology
-- see http://www.nist.gov/.

The difference of 0.010 m between both values is equivalent to 21km s. In any case, until this ambiguity is resolved, users should view their line velocity measurements of the 145.5 m [O I] line with caution.

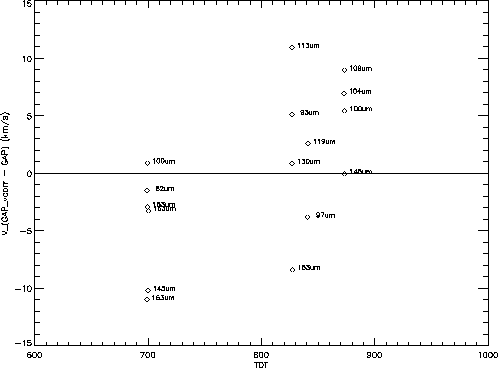
Another systematic check of the accuracy of the FPL calibration was made using 16 CO lines observed in Orion BN/KL between revolutions 699 and 873. The systematic error indicated above was evident, but to a lesser extent. Once the source velocity was subtracted (+ 9  km s, Knapp et al. 1981, [23]), the residual velocity differences (i.e. observed wavelength minus rest wavelength, expressed as velocity) have an rms of 6 km s and are never worse than 11 km s, as shown in Figure 5.27. This figure can provide some guidance to users on the magnitude and time-dependent nature of systematic errors observed in well calibrated LWS FPL data.

Figure 5.27: Velocity residuals measured for 16 CO lines in Orion. The dispersion of these residuals gives an idea of the wavelength accuracy for FPL.

For the accuracy of FPL measurements, we therefore adopted the most conservative value, half of the spectral resolution element or 13km s even if the internal scatter of data points seem to imply that a better accuracy could potentially be achieved. For FPS data the accuracy adopted is of a spectral resolution element or 6 km s.