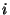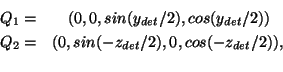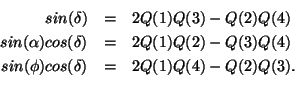



Next: 8.4 Photometry
Up: 8. Data Processing Level:
Previous: 8.2 PHT Auto Analysis
Subsections
8.3 Common Processing Steps
8.3.1 Read SPD header
Operation: Extract all relevant data from the SPD header.
The keywords from the SPD FITS header are read and stored internally for
processing. The information is eventually passed to the AAR product headers.
The following items are extracted from the SPD, the symbols in parenthesis
will be used in the remainder of this chapter:
- General SPD header keywords:
- EOHAAOTN, AOT name (e.g. P03)
- ATTYPE, type of attitude operation (P, T, or R for
single pointing, tracking or raster observation, respectively)
- DETECTOR, detector used
- NMEAS, number of measurements
- PTOREXT, point or extended source expected
- FPCMODE, chopper mode used
- FPCAMP, chopper amplitude [arcsec]
- CALSEQU, calibration sequence
- Spacecraft attitude data:
- CINSTRA, corrected reference instrument J2000 right ascension
in degrees (
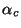 )
)
- CINSTDEC, corrected reference instrument J2000 declination
in degrees (
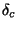 )
)
- CINSTROLL, corrected reference instrument J2000 roll angle
in degrees (
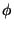 )
)
- in case a raster mode was executed:
- ATTRNPTS, number of raster points (M)
- ATTRNLNS, number of raster lines (N)
- ATTRDPTS, increment between points (dM)
- ATTRDLNS, increment between lines (dN)
- ATTRROTA, raster rotation angle
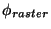
- Chopper mode information if FPCMODE is not staring:
- FPCNSTEP, number of chopper steps
- FPCINCR, increment between steps
- Spectrophotometric mode information if PHT40 used; for each pixel:
- LAMBDA, LUNC, the central wavelengths and uncertainty
- if point source: RESPP, RPUNC, point source responsivity
and uncertainty -
(
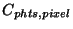 ,
,
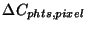 )
)
- if extended source: RESPE, REUNC, extended source responsivity
and uncertainty -
(
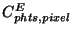 ,
,
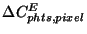 )
)
- CALDATE, date of production of spectral response function
- Results of SPD aperture photometry analysis, if PHT04 used:
- BACKSRSS, (logical) true if SPD aperture photometry
analysis could be applied
- NORMCALC, (logical) true if sufficient S/N
- FILTCORF, (logical) true if empirical aperture
correction factor was available
- NRMSIG
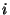 , relative background subtracted source flux ratio for
aperture
, relative background subtracted source flux ratio for
aperture 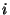
- NRMSIGU
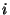 , uncertainty in ratio for aperture
, uncertainty in ratio for aperture 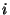
- Information for remaining AOTs; for each filter:
- FILTER, filter identification
- EXFLUX, expected flux density
- UNCFLX, uncertainty in expected flux density
- MXBACK, maximum expected background
- Detector responsivity related flags from SPD:
- RESPDEF, (logical) true if default responsivity was used.
- FCSDRIFT, (logical) true if signal of FCS measurement
contained a residual drift.
SPD product
8.3.2 Read SPD record
Operation: Extract necessary information from an SPD
record.
The following data are taken from each SPD record:
- Instrument time key (ITK)
- Raster point identifiers
- Filter identifier
- Aperture identifier
- Polariser identifier
- Number of destructive readouts
- Chopper plateau length (chopper dwell time) [1/128 s]
- Chopper step number
- Chopper position
- Measurement time [s]
- Measured powers plus uncertainties in [W] if PHT-P, PHT-C
- Measured flux densities plus uncertainties in [Jy] if PHT-S
- Plateau length [1/128 s]
- Data quality flags
For PHT-C and PHT-S, power, uncertainty, plateau length, and quality flags
refer to each pixel separately. The chopper step number is used to check
that an on-source and off-source pair are available for each chopped
measurement in the AA processing.
SPD product
8.3.3 Determine celestial coordinates of each pixel in record
Operation: For all SPD records, derive:
(1) the sky position (in RA and Dec) of the detector origin, and
(2) the RA and Dec offsets (in arcsec) for each detector pixel with respect
to the raster centre.
For a given SPD record, the position of a pixel on the sky is
determined by:
- the pixel's position in the detector array;
- a deflection of the focal plane chopper, by design the deflection is
only in the spacecraft Y direction;
- application of the raster mode, the raster mode can be defined either
in spacecraft reference coordinates (i.e. raster increments only in
Y and Z directions) or equatorial coordinates (raster increments in
RA and Dec directions).
All three instances can occur during the same measurement in case of AOT
PHT32 where the chopper is performing a saw-tooth scan using one of the
C-arrays while the spacecraft is rastering in spacecraft reference
coordinates.
For single pointing photometry the pointing keywords in the SPD product
header (Section 8.3.1) are used.
For raster maps the PHT OLP software will determine for each SPD record the
equatorial coordinates of the PHT centre field of view thereby considering
the raster position as well as a possible chopper deflection. Subsequently,
the RA and Dec offsets in arcseconds with respect to the centre of the map or
image coordinates are computed. The map centre has been provided by the
observer. Finally, the image coordinates for each pixel are derived taking
into account the individual pixel offsets and the spacecraft roll angle.
8.3.3.2 Extracting pointing data from IRPH
The instrument reference pointing history (IRPH) contains pointing
information expressed in quaternions (see `ISO Handbook, Vol. I: ISO -
Mission & Satellite Overview', [20]).
The quaternion  that defines the position of the PHT
central field of view for a given raster point in the J2000 inertial
frame can be computed from:
that defines the position of the PHT
central field of view for a given raster point in the J2000 inertial
frame can be computed from:
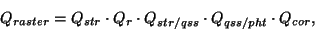 |
(8.1) |
where quaternions
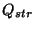 defines the J2000 pointing of the ISO star
tracker,
defines the J2000 pointing of the ISO star
tracker,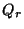 defines the raster point relative to the raster
centre of the scan,
defines the raster point relative to the raster
centre of the scan,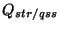 describes the misalignment between the
star tracker and the quadrant star sensor (QSS),
describes the misalignment between the
star tracker and the quadrant star sensor (QSS),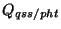 describes the QSS to instrument aperture alignment;
there is one value for
describes the QSS to instrument aperture alignment;
there is one value for 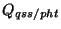 per PHT subsystem and is
listed in the focal plane geometry Cal-G file IFPG.FITS
(see `ISO Handbook, Vol. I: ISO - Mission & Satellite Overview',
[20]),
per PHT subsystem and is
listed in the focal plane geometry Cal-G file IFPG.FITS
(see `ISO Handbook, Vol. I: ISO - Mission & Satellite Overview',
[20]),  gives a fine pointing correction to the star tracker
calibration; since this correction depends on the position of the
guide star in the star tracker field of view, a different correction
is given for each raster position.
gives a fine pointing correction to the star tracker
calibration; since this correction depends on the position of the
guide star in the star tracker field of view, a different correction
is given for each raster position.
The following records are read from the IRPH:
- ATTMISQ(1:4), =
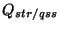 , star tracker to QSS
misalignment quaternion
, star tracker to QSS
misalignment quaternion
- ATTINSQ(1:4), =
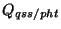 , QSS to instrument aperture
misalignment quaternion
, QSS to instrument aperture
misalignment quaternion
A more detailed description on the contents of the IRPH is given
in `ISO Handbook, Vol. I: ISO -
Mission & Satellite Overview', [20].
Note: due to different conventions adopted for the misalignment, Q(str/qss)
as given in the IRPH should be converted to the PHT OLP convention:
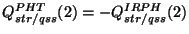
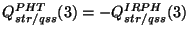
For each raster record in the IRPH, the following parameters are
extracted:
- raster point ID (RPID)
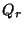 , raster point quaternion (RPQ)
, raster point quaternion (RPQ)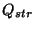 , star tracker quaternion (STRQ)
, star tracker quaternion (STRQ) , raster point correction quaternion (CORQ)
, raster point correction quaternion (CORQ)
With this information the quaternion  in
Equation 8.1 can be derived.
in
Equation 8.1 can be derived.
We define the detector origin to be the centre of the aperture
in case of a P detector, the centre of the central pixel 5 in case
of C100, and the centre of the array in case of C200.
Assuming a perfect alignment between chopper and spacecraft y-axis, the
quaternions representing the rotations of the detector origin with respect
to a given raster point are:
where 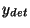 is the chopper deflection and
is the chopper deflection and 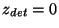 is the
spacecraft z-offset.
is the
spacecraft z-offset.
The quaternion of the detector origin for a given chopper position in a
raster can now be computed via:
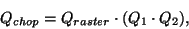 |
(8.2) |
where  is the raster point quaternion as derived in
Equation 8.1.
is the raster point quaternion as derived in
Equation 8.1.
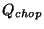 can be converted to RA (
can be converted to RA (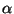 ),
Dec (
),
Dec (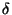 ), and Roll-angle (
), and Roll-angle (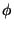 ) according to standard quaternion
transformation:
) according to standard quaternion
transformation:
8.3.4 Determination of the equatorial offsets of the detector centre
We define the detector centre to be the centre of the aperture
in case of PHT-P or the centre of a detector pixel in case of PHT-C. Note
that for PHT-P the detector origin and centre are identical.
Based on the position of the detector origin the detector centre
is obtained.
For a given record the sky position in RA and Dec of the detector origin is
converted into offsets (
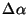 and
and
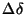 ) with respect
to the centre of the raster (
) with respect
to the centre of the raster (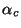 ,
, 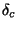 ). The offsets are
aligned with the RA and Dec axes in the equatorial coordinate system.
). The offsets are
aligned with the RA and Dec axes in the equatorial coordinate system.
For each pixel the RA and Dec offsets with respect to the detector origin
are computed from the detector roll angle and the relative pixel positions.
It is assumed that the pixels are positioned in an idealized configuration:
- the pixels in the C100 array are arranged in a regular
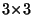 grid with
grid with 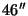 spacings in spacecraft Y and Z direction and
with the centre of pixel 5 in the origin at (
spacings in spacecraft Y and Z direction and
with the centre of pixel 5 in the origin at (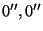 );
);
- the pixels in the C200 array are arranged in a regular
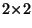 grid with
grid with  spacings in Y and Z direction. The origin is at
the centre of the array;
spacings in Y and Z direction. The origin is at
the centre of the array;
- in case of PHT-P the detector centre is the detector origin.
Adding the offsets of the detector origin this will give the map offsets
in arcsec for any raster position, detector pixel, and chopper plateau
combination.
- SPD product
- IRPH product




Next: 8.4 Photometry
Up: 8. Data Processing Level:
Previous: 8.2 PHT Auto Analysis
ISO Handbook Volume IV (PHT), Version 2.0.1, SAI/1999-069/Dc
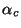 )
)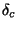 )
)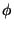 )
)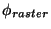
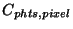 ,
,
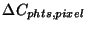 )
)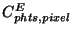 ,
,
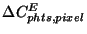 )
)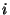 , relative background subtracted source flux ratio for
aperture
, relative background subtracted source flux ratio for
aperture 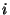
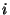 , uncertainty in ratio for aperture
, uncertainty in ratio for aperture