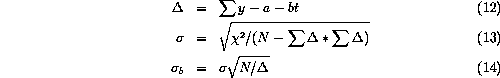This explanations are based on Do Kesters paper ``The calculation of
slopes'', dated 4 Jan 96)
To calculate the slope in the ISO detector data, we take the AC-corrected detector outputs for every reset interval, y, versus time, t. These should fit the equation one. Be aware that due to uncertainties in the AC-constants of every detector the slope might be slightly curved. This method to compute the error could give a sigma value even if the input before AC-correction is perfect. So the computed error is not suited to compare between detectors, moreover it represents the relative error of one detector.
where a is the offset (in microvolts) and b is the slope (in microvolts per
second) of one reset interval. As usual we write the 
-equation as
In the first instance the summation is over one second of data. Later, the
equation can be resummed over the complete reset interval. We want to
find a minimum in . To this end we differentiate the equation to
a and b and put both equations to 0: the normal equations.
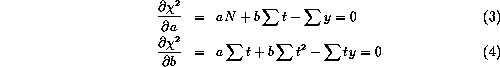
N : number of samples in 1 reset period
The solutions to this set of equations is
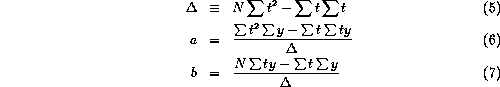
And:
The variance of the solution is 
and hence the standard
deviation is:
N : number of samples
We can now calculate the formal errors in the offset and the slope.
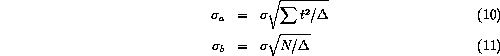
The `standard deviation of the slope', 
was passed into the SPD
product in field SWSPSTDV for OLP version 5.x.
Pipeline version 6.0 computes a slightly different `standard deviation of
the slope', :
