Next: 5.4 Detector Noise & Up: 5. Instrumental Characteristics Previous: 5.2 Grating Performance Overview

5.3 Fabry-Pérot Overview

The SWS Fabry-Pérot section may be used at wavelengths between 11.4 and 44.5 $\mu m$ . Instrument levels tests showed that performance in the extended wavelength range outside the nominal design wavelength range of 15-35 $\mu m$ was good enough to make the extended range available. A few remaining peculiarities of the extended range are discussed together with the following performance description. Results throughout this section refer to use of the Fabry-Pérot AOT bands of Table 3.2 that have been selected to give the best tradeoff between the various design goals (high sensitivity, low leakage etc.).

5.3.1 Spectral Resolution

The Fabry-Pérot spectral resolution was measured at a few discrete wavelengths using solid state laser sources. Fig. 5.1 shows the spectral resolution as a function of wavelength, interpolated between these measurements. The spectral resolution decreases towards the short wavelength ends of the wavelength ranges covered by the two Fabry-Pérots, where the wavelengths corresponding to the resonances of the reflective meshes are approached.

**Figure 5.1:** SWS Fabry-Pérot spectral resolution as a function of wavelength, computed from measured mesh properties and confirmed by checks at selected wavelengths
$\begin{figure} \begin{tabular}{c} \centerline{\epsfig{file={5_9.eps},width=15.0cm, angle=-90}}\\ \end{tabular}\end{figure}$

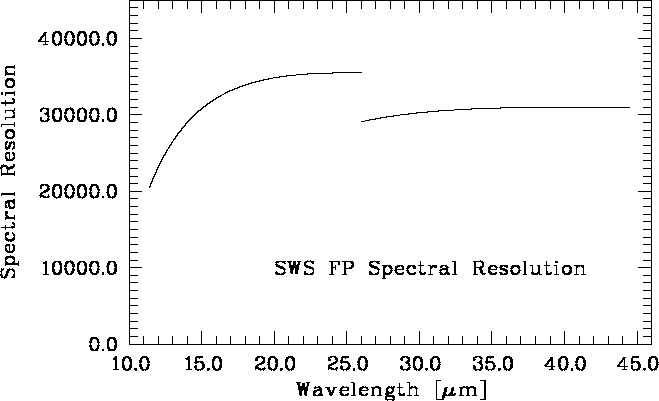
The Fabry-Pérot spectral resolution depends on precise parallelity of the F-P plates. An in-orbit spectral resolution very close to Figure 5.1 was obtained after execution of the in-orbit parallelisation procedure of the SWS F-P.

5.3.2 Sensitivity

The F-P sensitivity was characterized in instrument levels tests by doing measurements on a calibrated blackbody source within the test cryostat. Fig. 5.2 shows the SWS Fabry-Pérot spectral response. The conversion between units applicable to astronomical sources (Flux density of a point source in Jy) and the resulting instrumental signal ( $\mu$ V/s) is given as a function of wavelength. Diffraction losses caused by the fact that the aperture is comparable in size to the ISO diffraction disk have been taken into account; the flux used to derive Fig. 5.2 is the true point source flux. The effect of these diffraction losses is however not large (Fig. 5.3).

**Figure 5.2:** SWS Fabry-Pérot spectral response. The flux scale corresponds to a point source, diffraction losses at the aperture have been taken into account
$\begin{figure} \begin{tabular}{c} \centerline{\epsfig{file={5_10.eps},width=15.0cm}}\\ \end{tabular}\end{figure}$

The spectral response curve has structure on various wavelength scales. Large scale trends are determined by the counteracting effects of detector spectral response increasing with wavelength until close to the detector cut-off wavelength, and decreasing transmission of the Fabry-Pérot interferometer. Structures on scales of microns or tenths of microns can be traced to the detector spectral response curves and filter transmission curves. A rapid low-amplitude modulation in the 11.4-16 $\mu m$ range (not resolved in Fig. 5.2) is caused by reflections between the surfaces of the transmission filter used behind slit 1 in the long-wavelength section of SWS. This `parasitic Fabry-Pérot' effect is also observed for grating data using the same slit. The stronger modulation detected at $\lambda\geq 40$ $\mu m$ in the long-wavelength extended range is again caused by a parasitic Fabry-Pérot effect, this time in a reflecting CaF₂ filter. The nearby reststrahlen resonance of CaF₂ causes strong variations with wavelength of the indices of refraction and absorption, leading to the observed modulation pattern. The modulations were characterized with sufficient accuracy to allow good flux calibration in the extended wavelength ranges.

**Figure 5.3:** Computed ISO diffraction losses for the SWS F-P channels. The fraction of the ISO diffraction disk accepted by the effective SWS F-P aperture is shown as a function of wavelength
$\begin{figure} \begin{tabular}{c} \centerline{\epsfig{file={5_11.eps},width=15.0cm, angle=-90}}\\ \end{tabular}\end{figure}$

5.3.3 Noise

Measurements of noise for various reset intervals and signal levels during the SWS instrument level tests resulted in the following characterization of the noise behaviour of the F-P detector and integrating preamplifier system:

Noise at low signal levels is independent of signal. Here, noise as a function of reset interval can be approximately modelled as the quadratic sum of a constant read noise term and a dark current noise term increasing with time. Deviations from this model exist but may be ignored for simple sensitivity estimates
At higher signal, SNR improves only with the root of the signal, indicating dominance of shot noise.

For sensitivity calculations, this may be summarized as

$\begin{displaymath} N[\mu{}V/s] = \frac{\sqrt{N_R^2+(N_D^2+N_S^2S)t_r}}{t_r} \end{displaymath}$

with S the signal in $\mu$ V/s and t_r dimensionless (happens to be equal to the reset interval in seconds). The empirically determined noise parameters N_R (read noise, in $\mu$ V/s) N_D (dark current noise, in $\mu$ V/s), and N_S (signal shot noise, $\mu$ V^0.5/s^0.5) for the two F-P detector materials are summarized in Table 5.3.

**Table 5.3:** Fabry-Pérot noise parameters
Band	5	6
detector	FP-Si:Sb	FP-Ge:Be
range ( $\mu m$ )	11.4-26	26-44.5
$\rm N_R$	0.63	0.89
$\rm N_D$	1.00	3.00
$\rm N_S$	0.18	0.13

5.3.4 Saturation

No saturation problems are expected for the SWS Fabry-Pérot detectors. The saturation limit is given by the fact that the integration ramp for 1s detector reset interval does not hit the saturation level of the warm electronics for signals less than about 20,000 $\mu$ V/s. Although not foreseen in the current design of the offline data processing, it is in principle possible to obtain data for signals about seven times stronger by analysis of partial integration ramps. It is assumed here that the expected strong flux has been correctly specified in the AOT input, since only then the gain and reset time are set properly. Taking typical values from Fig. 5.1 and Fig. 5.2, the 20,000 $\mu$ V/s limit corresponds to a saturating flux density of about 2 x 10⁶ Jy, or a saturating flux in an unresolved line of about 10^-11 Wm^-2.

5.3.5 Leakage

The Fabry-Pérot section uses the grating as an order sorter that suppresses unwanted F-P orders. This suppression is not complete for part of the SWS wavelength range. Neighbouring F-P orders `leak' through the wings of the grating instrumental profile, contributing significantly to the total measured signal (See Figure 5.4). For observations of a single line superposed on a smooth continuum, the only drawback of leakage is a more complicated flux calibration, since leakage will increase the observed continuum but not the line. More serious effects occur in crowded spectra, where strong lines seen in the `wrong' F-P order may significantly distort the observed spectrum, requiring observations of wider wavelength ranges in order to determine the severity of this effect and `clean' the spectrum (See Fig. 5.6).

Leakage has been quantified by analysis of the grating instrumental profile as seen by the F-P detectors in scans of solid state laser lines. Figure 5.5 shows the leakage as a function of wavelength. It must be considered preliminary, since it is based on extrapolating the grating instrumental profile from measurements only at a few wavelengths of laser lines.

The spectral response data in section 5.2.2 have not been corrected for the effects of leakage, i.e. they refer to the total signal.

**Figure 5.4:** Basics of leakage in F-P spectra. The instrumental profile of the combination of F-P and grating is given by the solid line. Residual transmission from neighbouring F-P orders occurs if the instrumental profile of the grating alone (dashed line) is too wide
$\begin{figure} \begin{tabular}{c} \centerline{\epsfig{file={5_12.eps},width=15.0cm, angle=-90}}\\ \end{tabular}\end{figure}$

5.3.6 Tracking Noise

The coordination between Fabry-Pérot scans and the movement of the grating that tracks the F-P scan is a source of signature (or, loosely, `noise') that ultimately limits the quality of F-P spectra on bright sources. For all but very short F-P scans, the wavelength sampled by the F-P would soon be no longer tuned to the transmission peak of the grating if there were no tracking. The discrete steps of the grating's tracking movement result in the final F-P scan of a pure continuum source looking like a repetition of a small section of the grating instrumental profile.

The amplitude of this `noise' depends on various factors like quality of grating wavelength calibration, ratio between grating stepsize and line profile FWHM, pointing stability. It is hence difficult to predict for an observation at a certain wavelength. Instrument level tests with optimized grating wavelength calibration showed `signal-to-noise' around 200. In the case of an observation of a single line on a smooth continuum, part of the `noise' could be calibrated out by observing a larger region of continuum around the line, provided the non-systematic contribution of pointing jitter is not too large.

**Figure 5.5:** SWS Fabry-Pérot leakage. Leakage is defined here as the fraction of the total detected signal that originates in unwanted Fabry-Pérot orders. Preliminary data shown here are based on extrapolation from measurements at a few wavelengths.
$\begin{figure} \begin{tabular}{c} \centerline{\epsfig{file={5_13.eps},width=15.0cm, angle=-90}}\\ \end{tabular}\end{figure}$

**Figure 5.6:** Effects of leakage on a crowded spectrum. A wavelength range of high leakage has been selected for demonstration. The upper line shows the assumed true source spectrum at the SWS F-P spectral resolution, the lower line how it will appear in the presence of leakage.
$\begin{figure} \begin{tabular}{c} \centerline{\epsfig{file={5_14.eps},width=15.0cm, angle=-90}}\\ \end{tabular}\end{figure}$

Next: 5.4 Detector Noise & Up: 5. Instrumental Characteristics Previous: 5.2 Grating Performance Overview

SWS Instrument & Data Manual, Issue 1.0, SAI/98-095/Dc