The infrared wavelength range has borrowed units from the surrounding optical and radio (submm) regimes. Both magnitude and flux representations are widely used in the infrared.
Flux density ![]() of a source is defined as the flux per unit
frequency. Flux density is the physical unit used for point sources.
The unit of flux density is W m
of a source is defined as the flux per unit
frequency. Flux density is the physical unit used for point sources.
The unit of flux density is W m![]() Hz
Hz![]() . For practical
purposes in the infrared it is often convenient to scale this SI unit
and use Janskys (Jy) instead.
. For practical
purposes in the infrared it is often convenient to scale this SI unit
and use Janskys (Jy) instead.
| (A.1) |
ISOCAM-CVF and SWS spectra are given in units of Jy/pixel and Jy, respectively in AAR data products.
ISOPHOT-S spectra are given in units of W m![]() m
m![]() .
The conversion to Jy can be done in the following way:
.
The conversion to Jy can be done in the following way:
| (A.2) |
LWS spectra are given in units of ![]() W cm
W cm![]() m
m![]() .
The conversion to Jansky can be done with the following equation:
.
The conversion to Jansky can be done with the following equation:
| (A.3) |
For extended objects, surface brightness ![]() is used instead
of flux density. Also background emission, for point sources, is
expressed in brightness units. Brightness is defined as the flux
density per unit solid angle. The unit of brightness is
W m
is used instead
of flux density. Also background emission, for point sources, is
expressed in brightness units. Brightness is defined as the flux
density per unit solid angle. The unit of brightness is
W m![]() Hz
Hz![]() sr
sr![]() , but in practice it is
often scaled to MJy sr
, but in practice it is
often scaled to MJy sr![]() .
.
| (A.4) |
The flux density of a point source, in particular for a stellar object,
is often given in magnitudes ![]() . In the ISO wavelength range these
units are mostly used for ground based measurements below 20
. In the ISO wavelength range these
units are mostly used for ground based measurements below 20![]() m.
The conversion to or from magnitudes is performed via the
definition of the zero magnitude
flux density
m.
The conversion to or from magnitudes is performed via the
definition of the zero magnitude
flux density ![]() , which depends on the wavelength and on the
photometric system used. In the case of ISO, the system zero point is
defined by the model spectral energy distribution of Vega
(
, which depends on the wavelength and on the
photometric system used. In the case of ISO, the system zero point is
defined by the model spectral energy distribution of Vega
(![]() Lyr), available from http://www.iso.vilspa.esa.es/.
Lyr), available from http://www.iso.vilspa.esa.es/.
The magnitude ![]() of a ground based observation
can then be converted into flux density through the formula
of a ground based observation
can then be converted into flux density through the formula
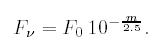 |
(A.5) |
For spectroscopic measurements, the total flux ![]() of a line is often
the most interesting quantity. A flux calibrated spectrum may be
presented in the form of flux density
of a line is often
the most interesting quantity. A flux calibrated spectrum may be
presented in the form of flux density
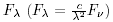 ) as a function of
wavelength
) as a function of
wavelength ![]() . Flux
. Flux ![]() of a line of interest can be obtained by
subtracting an appropriate continuum flux density level of the
spectrum before integrating over the entire line in wavelength
of a line of interest can be obtained by
subtracting an appropriate continuum flux density level of the
spectrum before integrating over the entire line in wavelength ![]() .
The unit of flux is Wm
.
The unit of flux is Wm![]() .
.