F.2 Long Term Transient Correction

Unlike the short term transient, no analytical or physical description has been developed so far to correct the LTT which seems to be a general behaviour of the ISOCAM detectors. Here we show how to correct the LTT by a least square minimization technique that makes use of the spatial redundancy of raster type observations.

For a given pixel at a position 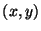$(x,y)$ on the detector array and at a given time $t$, the observed flux $I_{obs}(x,y,t)$ is related to the temporally varying flat-field $F(x,y,t)$, the incident flux $I_{sky}(x,y,t)$ and the long term drift $\Delta(t)$ by the following equation:

$$I_{obs}(x,y,t) = F(x,y,t)~I_{sky}(x,y,t) + \Delta(t).$$ (F.1)

Here we suppose that $\Delta(t)$ is not pixel dependent.

The offset function $\Delta(t)$ is found using equation F.1 and the spatial redundancy inherent to raster mode observations. We determine $\Delta(t)$ by solving a set of linear equations obtained by comparing flat-field corrected intensities of the same sky positions but obtained at different times.

The function of interest $\Delta(t)$ is estimated by minimizing the following criterion:

$$\chi^2 = \sum_{\alpha, \delta, t_i, t_j} \left[\frac{I_{obs}(\alpha, \delt... ...lta, t_i)} - \frac{I_{obs}(\alpha, \delta, t_j)}{F(\alpha, \delta, t_j)}\right.$$ (F.2)

$$- \left.\frac{\Delta(t_i)}{F(\alpha, \delta, t_i)} + \frac{\Delta(t_j)}{F(\alpha, \delta, t_j)} \right]^{2}$$

Here the sum is over all the possible pixel pairs that have seen the same region of the sky. The function $\Delta(t)$ is found by solving the linear system determined by the equation:

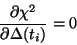$$\frac{\partial\chi^2}{\partial\Delta(t_i)} = 0$$ (F.3)

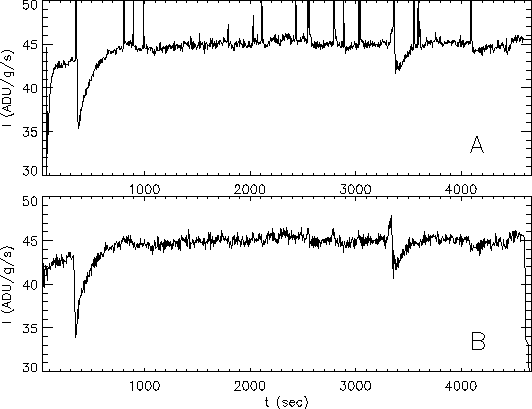
Figure F.2: Temporal evolution of a typical pixel. A) Raw data - many energetic electrons have hit the pixel causing instantaneous flux steps known as fast glitches. A response change is apparent near $t=350$ seconds caused by an ion impact (slow glitch). B) Fast glitches corrected data - short time flux steps have been identified as glitches and removed from the data cube. The glitch impact is removed correctly by the standard deglitching algorithm (Starck et al. 1999a, [58]) but the detector response is significantly disrupted for more than 500 seconds. These glitches with a memory effect are responsible for most of the periodic patterns seen in Figure F.3a. Such memory effects also occur after the observation of strong point sources.

The details of this correction can be found in Miville-Deschênes et al. 2000, [41]. The sky image of the first GRB observation, obtained after the LTT correction, is shown in Figure F.3b. At this stage we have used a single flat-field to compute the sky image. However, it is still necessary to use a variable flat-field to correct the artefacts (e.g. periodic patterns) seen in Figure F.3b.

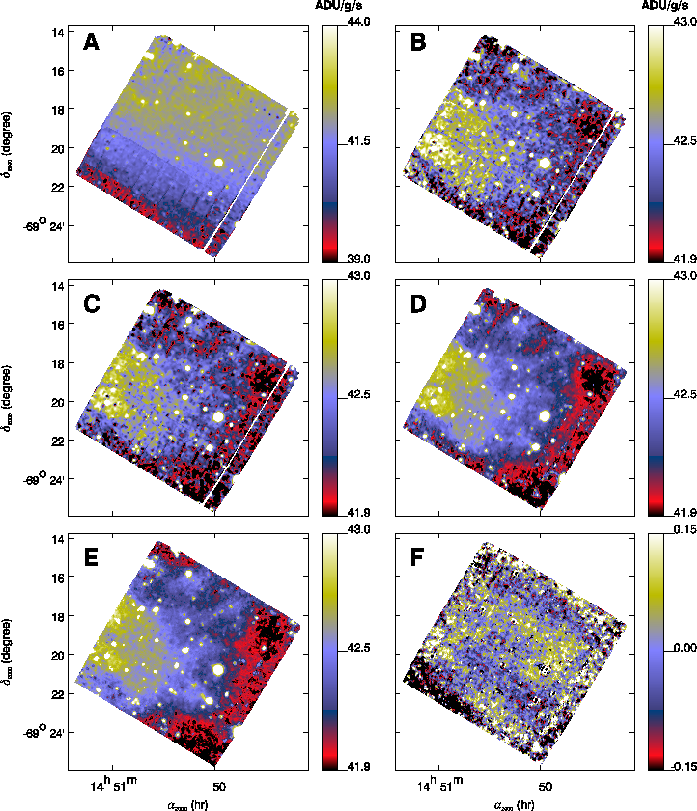
Figure F.3: LW10 images of the first GRB970402 observation after deglitching, dark subtraction, transient correction (A), long term transient correction (B), variable flat-field (C) and bad pixel removal (D). Image (E) is the final map of the second GRB970402 observation and image (F) is the difference between (D) and (E). For these observations, 1 ADU/G/s corresponds to 0.242 mJy/pix or 0.286 MJy/sr.