In this section we first describe the extraction of the source signal from [source+background] and background signal. Subsequently the flux calibration for PHT-S is presented.
Detailed description: none
The average signal per chopper plateau is obtained by applying processing steps 7.3.4 (deglitching), 7.3.5 (drift recognition), and 7.3.6 (mean signal per plateau).
None
Detailed description: none
The background subtraction for a given chopper cycle and chopper mode is performed in this step.
For a given chopper cycle the background signal is subtracted from the [source+background] signal to obtain the source signal. This operation is repeated until the end of a measurement is encountered. Weighting factors are derived from the uncertainties which are used for the averaging of all chopper cycles at the end of a measurement.
In the following we describe the background subtraction method
for the different chopper modes. Note that each cycle in triangular
chopping mode consists of 4 plateaux referring to 2 [source+background]
and 2 different background positions. In sawtooth mode there are 3 plateaux:
1 [source+background] and two different background positions.
The following symbols are used for chopper cycle ![]() :
:
All signals are given in V/s, the weights are dimensionless.
Each cycle contains only 1 [source+background] plateau and 1
reference background position. For chopper cycle ![]() :
:
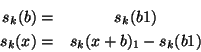
The weighting factor is determined from the signal uncertainties:
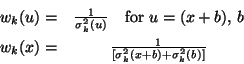
where ![]() is the uncertainty in signal for the measurement
on [source+background], etc.
is the uncertainty in signal for the measurement
on [source+background], etc.
Each chopper cycle contains 1 [source+background] chopper plateau
and 2 reference positions. For chopper cycle ![]() :
:
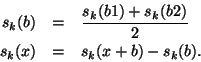
With weighting factors:
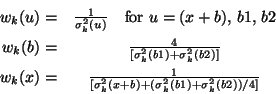
where
![]() is the uncertainty in the signal for the measurement
on [source+background], etc.
is the uncertainty in the signal for the measurement
on [source+background], etc.
Each chopper cycle contains 2 [source+background] chopper plateaux
and 2 reference positions. For chopper cycle ![]() :
:
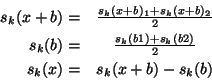
A weighting factor is also determined from the power uncertainties:
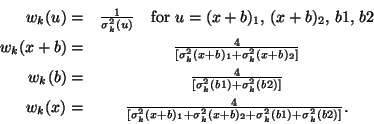
Detailed description: none
The average source and background signals of all chopper cycles in a measurement is determined.
For all chopper cycles in a measurement, the weighted average is computed
from the parameters per chopper cycle. For a given set of signals
![]() with weights
with weights ![]() obtained over a measurement, the weighted
mean
obtained over a measurement, the weighted
mean ![]() and its associated uncertainty
and its associated uncertainty ![]() is computed
according to Equation 7.20. The mean can be either the
signal of the source or background.
is computed
according to Equation 7.20. The mean can be either the
signal of the source or background.
In rectangular mode the following mean signals are derived for each pixel:
In sawtooth and triangular mode the following mean signals are derived for each pixel:
Detailed description: Section 5.2.6
Analysis of chopped PHT-S data obtained from standard stars have shown that the PHT-S spectral response function is not unique but depends on the brightness of the source due to chopped signal losses. It is found that the amount of signal loss in a given detector pixel strongly depends on the source brightness in that pixel.
An accurate spectral response function ![]() for pixel
for pixel ![]() is
obtained by assuming an average spectral response function which
is corrected per pixel for a source dependent signal loss:
is
obtained by assuming an average spectral response function which
is corrected per pixel for a source dependent signal loss:
with
where the superscripts ![]() refer to a chopped observation, and
refer to a chopped observation, and ![]() to a point source, and
to a point source, and
The Cal-G file
PSPECAL contains the average spectral response
functions for both staring and chopped mode observations of point
and extended sources, see Section 14.19.1.
The file includes also the first order correction factors (
![]() ).
).
Detailed description: none
The chopped PHT-S spectral energy distribution for the source and [source+background] is computed using the spectral response function corrected for chopper losses:
| (7.62) | |||
| (7.63) |
with
| (7.64) | |||
| (7.65) |
The background spectrum is derived from the difference:
| (7.66) | |||
| (7.67) |
The resulting spectra are stored in the SPD products.
none